Volume 23 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
On 2-powerfully perfect numbers in three quadratic rings
Original research paper. Pages 1–11
Colin Defant
Full paper (PDF, 208 Kb) | Abstract
Using an extension of the abundancy index to imaginary quadratic rings with unique factorization, we define what we call
n-powerfully perfect numbers in these rings. This definition serves to extend the concept of perfect numbers that have been defined and studied in the integers. We investigate the properties of 2-powerfully perfect numbers in the rings

and

the three imaginary quadratic rings with unique factorization in which 2 is not a prime.
Conditions equivalent to the Descartes–Frenicle–Sorli Conjecture on odd perfect numbers
Original research paper. Pages 12–20
Jose Arnaldo B. Dris
Full paper (PDF, 156 Kb) | Abstract
The Descartes-Frenicle-Sorli conjecture predicts that k = 1 if qkn2 is an odd perfect number with Euler prime q. In this note, we present some conditions equivalent to this conjecture.
Study of some equivalence classes of primes
Original research paper. Pages 21–29
Sadani Idir
Full paper (PDF, 236 Kb) | Abstract
In this paper, we introduce an equivalence relation ~ on ℙ for studying some specific classes of prime numbers. This relation and the famous prime number theorem allows us to estimate the number of prime numbers of each equivalence class, the number of the different equivalence classes and to show some other results.
On solutions of the Diophantine equation 1/x1+2/x2+3/x3+…+k/xk=1 when 2 ≤ x1 < x2 < x3 < … < xk are integers and k = x1
Original research paper. Pages 30–35
Nechemia Burshtein
Full paper (PDF, 166 Kb) | Abstract
Some general solutions of the title equation are established and exhibited. It is also shown that for each value of x1 when x1 ≤ 4, the equation has at least three solutions. For the particular values x1 = 2, 3, 4, all the solutions of the equation are determined and demonstrated.
The primitive solutions to the Diophantine equation 2X4 + Y4 =Z3
Original research paper. Pages 36–44
Gustav Söderlund
Full paper (PDF, 181 Kb) | Abstract
We find all primitive non-zero integer solutions to the title equation, namely (x, y, z) =(±5,±3, 11). The proofs involved are based solely on elementary methods with no use of computers and the elliptic curve machinery.
The q-Lah numbers and the nth q-derivative of expq(1/n)
Original research paper. Pages 45–47
Jacob Katriel
Full paper (PDF, 145 Kb) | Abstract
A recently reported nice and surprising property of the Lah numbers is shown to hold for q-Lah numbers as well, i.e., they can be obtained by taking successive q-derivatives of expq(1/n), where expq(x) is the q-exponential.
On two arithmetic functions
Original research paper. Pages 48–53
József Sándor and Krassimir T. Atanassov
Full paper (PDF, 162 Kb) | Abstract
Some properties of two new arithmetic functions are studied. Three conjectures are formulated.
Fast converging series for zeta numbers in terms of polynomial representations of Bernoulli numbers
Original research paper. Pages 54–80
J. Braun, D. Romberger and H. J. Bentz
Full paper (PDF, 254 Kb) | Abstract
In this paper we introduce a new polynomial representation of the Bernoulli numbers in terms of polynomial sums allowing on the one hand a more detailed understanding of their mathematical structure and on the other hand provides a computation of B 2n as a function of B 2n − 2. Furthermore, we show that a direct computation of the Riemann zeta-function and their derivatives at k∈ Z is possible in terms of these polynomial representation. As an explicit example, our polynomial Bernoulli number representation is applied to fast approximate computations of ζ(3), ζ(5) and ζ(7).
Extensions of D’Aurizio’s trigonometric inequality
Original research paper. Pages 81–83
József Sándor
Full paper (PDF, 139 Kb) | Abstract
We offer extensions of D’Aurizio’s trigonometric inequality, as well to its counterpart, proved in
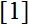
and
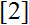
.
A conjecture on degrees of algebraic equations
Original research paper. Pages 84–90
Simon Davis
Full paper (PDF, 175 Kb) | Abstract
It is proven that the validity of a conjecture on the degrees of an algebraic equation consisting of three polynomials is determined by the derivatives. The result is extended to positive polynomials satisfying a generalized Fermat equation, after setting the exponents X, Y and Z equal to 1, and specialization to prime factors of the product of integer values of the polynomials yields the inequality equivalent to the abc conjecture.
On the Pell p-circulant sequences
Original research paper. Pages 91–103
Yeşim Aküzüm, Ömür Deveci, and A. G. Shannon
Full paper (PDF, 197 Kb) | Abstract
In this paper, we define the generalized Pell p-circulant sequence and the Pell pcirculant sequence by using the circulant matrices which are obtained from the characteristic polynomial of the generalized Pell (p,i)-sequence and then, we obtain miscellaneous properties of these sequences. Also, we consider the cyclic groups which are generated by the generating matrices and the auxiliary equations of the defined recurrence sequences and then, we study the orders of these groups. Furthermore, we extend the Pell p-circulant sequence to groups. Finally, we obtain the lengths of the periods of Pell p-circulant sequences in the semidihedral group SD2m for m ≥ 4 as applications of the results obtained.
Closed-form evaluations of Fibonacci–Lucas reciprocal sums with three factors
Original research paper. Pages 104–116
Robert Frontczak
Full paper (PDF, 189 Kb) | Abstract
In this article we present expressions for certain types of reciprocal Fibonacci and Lucas sums. The common feature of the sums is that in each case the denominator of the summand consists of a product of three Fibonacci or Lucas numbers.
On Legendre’s Conjecture
Original research paper. Pages 117–125
A. G. Shannon and J. V. Leyendekkers
Full paper (PDF, 179 Kb) | Abstract
This paper considers some aspects of Legendre’s conjecture as a conjecture and estimates the number of primes in some intervals in order to portray a compelling picture of some of the computational issues generated by the conjecture.
The extension of some D(4)-pairs
Original research paper. Pages 126–135
Alan Filipin
Full paper (PDF, 181 Kb) | Abstract
In this paper we illustrate the use of the results from
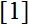
proving that
D(4)-triple {
a,
b,
c} with
a <
b <
a+57√
a has a unique extension to a quadruple with a larger element. This furthermore implies that
D(4)-pair {
a,
b} cannot be extended to a a quintuple if
a <
b <
a+57√
a .
Volume 23 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
 and
and  the three imaginary quadratic rings with unique factorization in which 2 is not a prime.
the three imaginary quadratic rings with unique factorization in which 2 is not a prime.


