Volume 26 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
On the equation φ(n) + d(n) = n and related inequalities
Original research paper. Pages 1–4
József Sándor
Full paper (PDF, 159 Kb) | Abstract
We study the equation φ(n) + d(n) = n, and prove related new inequalities.
Equalities between greatest common divisors involving three coprime pairs
Original research paper. Pages 5–7
Rogelio Tomás García
Full paper (PDF, 140 Kb) | Abstract
A new equality of the greatest common divisor (gcd) of quantities involving three coprime pairs is proven in this note. For ai and bi positive integers such that gcd(ai, bi) = 1 for i ∈ {1, 2, 3} and dij = |aibj − ajbi|, then gcd(d32; d31) = gcd(d32; d21) = gcd(d31; d21): The proof uses properties of Farey sequences.
Some modular considerations regarding odd perfect numbers – Part II
Original research paper. Pages 8–24
Jose Arnaldo Bebita Dris and Immanuel Tobias San Diego
Full paper (PDF, 181 Kb) | Abstract
In this article, we consider the various possibilities for
p and
k modulo 16, and show conditions under which the respective congruence classes for
σ(
m2) (modulo 8) are attained, if
pkm2 is an odd perfect number with special prime
p. We prove that
- σ(m2) ≡ 1 (mod 8) holds only if p + k ≡ 2 (mod 16).
- σ(m2) ≡ 3 (mod 8) holds only if p − k ≡ 4 (mod 16).
- σ(m2) ≡ 5 (mod 8) holds only if p + k ≡ 10 (mod 16).
- σ(m2) ≡ 7 (mod 8) holds only if p − k ≡ 4 (mod 16).
We express gcd(m2; σ(m2)) as a linear combination of m2 and σ(m2). We also consider some applications under the assumption that σ(m2) / pk is a square. Lastly, we prove a last-minute conjecture under this hypothesis.
On the quantity I(qk) + I(n2) where qk n2 is an odd perfect number
Original research paper. Pages 25–32
Jose Arnaldo Bebita Dris
Full paper (PDF, 194 Kb) | Abstract
In this note, we pursue an approach started in the M. Sc. thesis of the author and thereby attempt to produce stronger bounds for the sum I(qk) + I(n2), where qkn2 is an odd perfect number with special prime q and I(x) is the abundancy index of the positive integer x.
Bi-unitary multiperfect numbers, III
Original research paper. Pages 33–67
Pentti Haukkanen and Varanasi Sitaramaiah
Full paper (PDF, 319 Kb) | Abstract
A divisor d of a positive integer n is called a unitary divisor if gcd(d, n/d) = 1, and d is called a bi-unitary divisor of n if the greatest common unitary divisor of d and n/d is unity. The concept of a bi-unitary divisor is due to D. Surynarayana (1972). Let σ∗∗(n) denote the sum of the bi-unitary divisors of n. A positive integer n is called a bi-unitary multiperfect number if σ∗∗(n) = kn for some k ≥ 3. For k = 3 we obtain the bi-unitary triperfect numbers.
Peter Hagis (1987) proved that there are no odd bi-unitary multiperfect numbers. The present paper is part III in a series of papers on even bi-unitary multiperfect numbers. In parts I and II we found all bi-unitary triperfect numbers of the form n = 2au, where 1 ≤ a ≤ 5 and u is odd. There exist exactly six such numbers. In this part we examine the case a = 6. We prove that if n = 26u is a bi-unitary triperfect number, then n = 22848, n = 342720, n = 51979200 or n = 779688000.
On quasimultiperfect numbers
Original research paper. Pages 68–73
P. Anantha Reddy, C. Sunitha and V. Siva Rama Prasad
Full paper (PDF, 167 Kb) | Abstract
For a positive integer n, let σ(n) and ω(n) respectively denote the sum of the positive divisors of n and the number of distinct prime factors of n. A positive integer n is called a quasimultiperfect (QM) number if σ(n) = kn + 1 for some integer k ≥ 2. In this paper we give some necessary conditions to be satisfied by the prime factors of QM number n with ω(n) = 3 and ω(n) = 4. Also we show that no QM n with ω(n) = 4 can be a fourth power of an integer.
Notes on the Hermite-based poly-Euler polynomials with a q-parameter
Original research paper. Pages 74–82
Burak Kurt
Full paper (PDF, 206 Kb) | Abstract
We introduce and investigate the Hermite-based poly-Euler polynomials with a q-parameter. We give some basic properties and identities for these polynomials. Furthermore, we prove two explicit relations.
Bivariate Mersenne polynomials and matrices
Original research paper. Pages 83–95
Francisco Regis Vieira Alves
Full paper (PDF, 254 Kb) | Abstract
In this work we present a new notion called bivariate polynomials of Mersenne. We will also discuss certain related matrix properties. Finally, we introduce a notion of the bivariate quaternions of Mersenne.
Half self-convolution of the k-Fibonacci sequence
Original research paper. Pages 96–106
Sergio Falcon
Full paper (PDF, 202 Kb) | Abstract
We say the k-Fibonacci numbers Fk,i and Fk,j are equidistant if j = n − i and then we study some properties of these pairs of numbers. As a main result, we look for the formula to find the generating function of the product of the equidistant numbers, their sums and their binomial transforms. Next we apply this formula to some simple cases but more common than the general. In particular, we define the half self-convolution of the k-Fibonacci and k-Lucas sequences. Finally, we study the sum of these new sequences, their recurrence relations, and their generating functions.
A single parameter Hermite–Padé series representation for Apéry’s constant
Original research paper. Pages 107–134
Anier Soria-Lorente and Stefan Berres
Full paper (PDF, 285 Kb) | Abstract
Inspired by the results of Rhin and Viola (2001), the purpose of this work is to elaborate on a series representation for ζ(3) which only depends on one single integer parameter. This is accomplished by deducing a Hermite–Padé approximation problem using ideas of Sorokin (1998). As a consequence we get a new recurrence relation for the approximation of ζ(3) as well as a corresponding new continued fraction expansion for ζ(3), which do no reproduce Apéry’s phenomenon, i.e., though the approaches are different, they lead to the same sequence of Diophantine approximations to ζ(3). Finally, the convergence rates of several series representations of ζ(3) are compared.
A generalization to almost balancing and cobalancing numbers using triangular numbers
Original research paper. Pages 135–148
S. G. Rayaguru and G. K. Panda
Full paper (PDF, 206 Kb) | Abstract
A generalization of almost balancing numbers is studied using triangular numbers as the difference between the left and right hand sides of the defining equation of balancing
numbers. In case of almost balancing numbers, this difference is kept 1; which is the first triangular number. Some specific representations of these numbers in terms of balancing and balancing related numbers are established and few more results with triangular, square triangular, balancing and balancing related numbers are also studied so as to generalize the identities obtained by A. Tekcan.
Markov equation with components of some binary recurrent sequences
Original research paper. Pages 149–159
S. G. Rayaguru, M. K. Sahukar and G. K. Panda
Full paper (PDF, 211 Kb) | Abstract
The generalized Lucas sequence {Un}n≥0 is defined by Un+1 = rUn + sUn−1; n ≥ 0 with U0 = 0; U1 = 1 of which the Fibonacci sequence (Fn) is the particular case r = s = 1. In 2018, F. Luca and A. Srinivasan searched for the solutions x, y, z ∈ Fn of the Markov equation x2 + y2 + z2 = 3xyz and proved that (F1; F2n−1, F2n+1); n ≥ 1 is the only solution. In this paper, we extend this work from the Fibonacci sequence to any generalized Lucas sequence Un for the case s = ±1.
An identity involving Bernoulli numbers and the Stirling numbers of the second kind
Original research paper. Pages 160–162
Sumit Kumar Jha
Full paper (PDF, 123 Kb) | Abstract
Let
Bn denote the Bernoulli numbers, and
S(
n, k) denote the Stirling numbers of the second kind. We prove the following identity
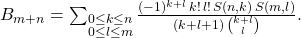
To the best of our knowledge, the identity is new.
On bicomplex generalized Tetranacci quaternions
Original research paper. Pages 163–175
Yüksel Soykan and Erkan Taşdemir
Full paper (PDF, 173 Kb) | Abstract
In this paper, we introduce the bicomplex generalized Tetranacci quaternions. Furthermore, we present some properties of these quaternions and derive relationships between them.
Hyperbolic k-Fibonacci and k-Lucas octonions
Original research paper. Pages 176–188
A. D. Godase
Full paper (PDF, 182 Kb) | Abstract
In this paper, we introduce the hyperbolic k-Fibonacci and k-Lucas octonions. We present Binet’s formulas, Catalan’s identity, Cassini’s identity, d’Ocagne’s identity and generating functions for the k-Fibonacci and k-Lucas hyperbolic octonions.
Identities on generalized Fibonacci and Lucas numbers
Original research paper. Pages 189–202
K. M. Nagaraja and P. Dhanya
Full paper (PDF, 205 Kb) | Abstract
In this article, the concepts of Fibonacci, Tribonacci, Lucas and Tetranacci numbers are generalized as continued sum. The generalized Fibonacci identity is proved by using induction and the binomial theorem. Further, it is proved that the generalized Fibonacci and Lucas sequences are logarithmically convex (concave) and some special identities are obtained.
Fibonacci–Lucas identities and the generalized Trudi formula
Original research paper. Pages 203–217
Taras Goy and Mark Shattuck
Full paper (PDF, 232 Kb) | Abstract
In this paper, we evaluate determinants of several families of Hessenberg matrices having Fibonacci numbers as their nonzero entries. By the generalized Trudi formula, these determinant identities may be written equivalently as formulas for the Lucas numbers in terms of the Fibonacci. We provide both algebraic and combinatorial proofs of our determinant results. The former makes use of expansion along columns and induction, while the latter draws upon the definition of the determinant as a signed sum over the symmetric group and uses parity-changing involutions.
On intercalated Fibonacci sequences
Original research paper. Pages 218–223
Krassimir T. Atanassov and Anthony G. Shannon
Full paper (PDF, 81 Kb) | Abstract
We construct three intercalated sequences and develop their essential properties which are generalizations of the three basic Fibonacci sequences. They are extensions of
pulsated sequences described at previous Fibonacci conferences. We relate these sequences to the sequence {yn}n ≥ 0 = {0, 1, 4, 15, 56,…}.
On the Padovan p-circulant numbers
Original research paper. Pages 224–233
Güzel İpek, Omür Deveci and Anthony G. Shannon
Full paper (PDF, 159 Kb) | Abstract
In this paper, we define Padovan p-circulant numbers by using circulant matrices which are obtained from the characteristic polynomials of the Padovan p-numbers. Then, we derive the permanental and the determinantal representations of the Padovan p-circulant numbers by using certain matrices which are obtained from the generating matrix of Padovan p-circulant sequence. Also, we obtain the combinatorial representation, the exponential representation and the sums of the Padovan p-circulant numbers by the aid of the generating function and the generating matrix of the Padovan p-circulant sequence.
A refinement of the 3x + 1 conjecture
Original research paper. Pages 234–244
Roger Zarnowski
Full paper (PDF, 265 Kb) | Abstract
The 3x + 1 conjecture pertains to iteration of the function T defined by T(x) = x/2 if x is even and T(x) = (3x + 1)/2 if x is odd. The conjecture asserts that the trajectory of every positive integer eventually reaches the cycle (2, 1). We show that the essential dynamics of T-trajectories can be more clearly understood by restricting attention to numbers congruent to 2 (mod 3). This approach leads to an equivalent conjecture for an underlying function TR whose iterates eliminate many extraneous features of T-trajectories. We show that the function TR that governs the refined conjecture has particularly simple mapping properties in terms of partitions of the set of integers, properties that have no parallel in the classical formulation of the conjecture. We then use those properties to obtain a new characterization of T-trajectories and we show that the dynamics of the 3x + 1 problem can be reduced to an iteration involving only numberscongruent to 2 or 8 (mod 9).
On the constant congruence speed of tetration
Original research paper. Pages 245–260
Marco Ripà
Full paper (PDF, 265 Kb) | Abstract
Integer tetration, the iterated exponentiation ba for a ∈ ℕ − {0, 1}, is characterized by fascinating periodicity properties involving its rightmost figures, in any numeral system. Taking into account a radix-10 number system, in the book “La strana coda della serie n ^ n ^ … ^ n” (2011), the author analyzed how many new stable digits are generated by every unitary increment of the hyperexponent b, and he indicated this value as V(a) or “congruence speed” of a ≢ 0 (mod 10). A few conjectures about V(a) arose. If b is sufficiently large, the congruence speed does not depend on b, taking on a (strictly positive) unique value. We derive the formula that describes
V(a) for every a ending in 5. Moreover, we claim that V(a) = 1 for any a (mod 25) ∈ {2, 3, 4, 6, 8, 9, 11, 12, 13, 14, 16, 17, 19, 21, 22, 23} and V(a) ≥ 2 otherwise. Finally, we show the size of the fundamental period P for any of the remaining values of the congruence speed: if V(a) ≥ 2, then P(V(a)) = 10V(a)+1.
This issue of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP1-15/2019.
Volume 26 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4


