Some modular considerations regarding odd perfect numbers – Part II

Jose Arnaldo Bebita Dris and Immanuel Tobias San Diego
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 26, 2020, Number 3, Pages 8–24
DOI: 10.7546/nntdm.2020.26.3.8-24
Full paper (PDF, 192 Kb)
Corrigendum (PDF, 159 Kb)

Details

Authors and affiliations

Jose Arnaldo Bebita Dris
M. Sc. Graduate, Mathematics Department
De La Salle University, Manila, Philippines 1004

Immanuel Tobias San Diego
Department of Mathematics and Physical Sciences
Trinity University of Asia, Quezon City, Philippines 1102

Abstract

In this article, we consider the various possibilities for p and k modulo 16, and show conditions under which the respective congruence classes for σ(m²) (modulo 8) are attained, if p^km² is an odd perfect number with special prime p. We prove that

1. σ(m²) ≡ 1 (mod 8) holds only if p + k ≡ 2 (mod 16).
2. σ(m²) ≡ 3 (mod 8) holds only if p − k ≡ 4 (mod 16).
3. σ(m²) ≡ 5 (mod 8) holds only if p + k ≡ 10 (mod 16).
4. σ(m²) ≡ 7 (mod 8) holds only if p − k ≡ 4 (mod 16).

We express gcd(m²; σ(m²)) as a linear combination of m² and σ(m²). We also consider some applications under the assumption that σ(m²) / p^k is a square. Lastly, we prove a last-minute conjecture under this hypothesis.

Keywords

• Sum of divisors
• Sum of aliquot divisors
• Deficiency
• Odd perfect number
• Special prime

2010 Mathematics Subject Classification

• 11A05
• 11A25

References

1. Broughan, K. A., Delbourgo, D., & Zhou, Q. (2013). Improving the Chen and Chen result for odd perfect numbers, Integers, 13, Article #A39.
2. Brown, P. A. (2016). A partial proof of a conjecture of Dris, preprint, https://arxiv.org/abs/1602.01591.
3. Chen, S.-C., & Luo, H. (2013). Odd multiperfect numbers, Bull. Aust. Math. Soc., 88 (1), 56–63.
4. Cohen, G. L., & Sorli, R. M. (2012). On odd perfect numbers and even 3-perfect numbers, Integers, 12A, Article #A6.
5. Dandapat, G. G., Hunsucker, J. L., & Pomerance, C. (1975). Some new results on odd perfect numbers, Pacific J. Math., 57 (2), 359–364.
6. Dris, J. A. B. (2008). Solving the odd perfect number problem: some old and new approaches, M. Sc. thesis, De La Salle University, Manila, Philippines.
7. Dris, J. A. B. (2017). On a curious biconditional involving the divisors of odd perfect numbers, Notes Number Theory Discrete Math., 23 (4), 1–13.
8. Dris, J. A. B. (2017). Conditions equivalent to the Descartes–Frenicle–Sorli conjecture on odd perfect numbers, Notes Number Theory Discrete Math., 23 (2), 12–20.
9. Dris, J. A.B., & San Diego, I.T. (2020). Some modular considerations regarding odd perfect numbers, Notes Number Theory Discrete Math., 26 (2), 27–33.
10. Dris, J. A. B., & MathStackExchange user FredH (2019). If 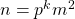is an odd perfect number with special prime 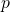, then 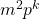is not a square. https://math.stackexchange.com/questions/3121498.
11. Ewell, J. A. Jr. (1980). On the multiplicative structure of odd perfect numbers, Journal of Number Theory, 12, 339–342.
12. Ochem, P. (2019). Answer to a question of the first author in Mathematics StackExchange, https://math.stackexchange.com/a/3151412/28816.
13. Sloane, N. J. A., OEIS sequence A033879 – Deficiency of n, or 2n − σ(n), https://oeis.org/A033879.
14. Sloane, N. J. A., & Guy, R. K., OEIS sequence A001065 – Sum of proper divisors (or aliquot parts) of n: sum of divisors of n that are less than n, https://oeis.org/A001065.
15. Starni, P. (2018). On Dris conjecture about odd perfect numbers, Notes Number Theory Discrete Math., 24 (1), 5–9.
16. Starni, P. (1991). On the Euler’s factor of an odd perfect number, Journal of Number Theory, 37, 366–369.
17. Wikipedia contributors. (2019, March 6). Perfect number. In Wikipedia, The Free Encyclopedia. Retrieved from https://en.wikipedia.org/w/index.php?title=Perfect_number&oldid=886493275.