Volume 26 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Riemann zeta function and arithmetic progression of higher order
Original research paper. Pages 1–7
Hamilton Brito, Éder Furtado and Fernando Matos
Full paper (PDF, 567 Kb) | Abstract
Riemann zeta function has a great importance in number theory, constituting one of the most studied functions. The zeta function, being a series, has a close relationship with the arithmetic progressions (AP). AP of higher order allows the understanding of several probabilities involving sequences. In this paper, we will approach Riemann zeta function with an AP of higher order. We will deduce a formula from the progression that will allow to express of the zeta function for a natural number greater than or equal to 2. In this way, we will show that the study of an AP of higher order can be very useful in the study of Riemann zeta function, and it may open other possibilities for studying the value of this function for odd numbers.
Odd and even repetition sequences of independent domination number
Original research paper. Pages 8–20
Leomarich F. Casinillo
Full paper (PDF, 659 Kb) | Abstract
Let {Pn}n=1∞ be a sequence of paths. The odd repetition sequence denoted by {𝜌𝑘𝑜:𝑘∈ℕ} is a sequence of natural numbers in which odd numbers are repeated once and defined by {𝜌𝑘𝑜}={1,1,2,3,3,4,5,5,…}={𝑖(𝑃𝑛)} where 𝑛=2𝑘−1. The even repetition sequence denoted by {𝜌𝑘𝑒:𝑘∈ℕ} is a sequence of natural numbers, in which even numbers are repeated once and defined by {𝜌𝑘𝑒}={1,2,2,3,4,4,5,6,6,…}={𝑖(𝑃𝑛)}, where 𝑛 = 2𝑘. In this paper, the explicit formula that shows the values of the element of two sequences {𝜌𝑘𝑜}} and {𝜌𝑘𝑒} that depends on the subscript 𝑘 were constructed. Also, the formula that relates the partial sum of the elements of the said sequences, which depends on the subscript 𝑘 and order of the sequence of paths, were established. Further, the independent domination number of the triangular grid graph 𝑇𝑚 = (𝑉(𝑇𝑚), 𝐸(𝑇𝑚)) will be determined using the said sequences and the two sequences will be evaluated in relation to the Fibonacci sequence {𝐹𝑛} along with the order of the path.
Square-full numbers with an even number of prime factors
Original research paper. Pages 21–30
Rafael Jakimczuk
Full paper (PDF, 183 Kb) | Abstract
In this article, we study the functions ω(n) and Ω(n), where n is an s-full number. For example, we prove that the square-full numbers with Ω(n) even are in greater proportion than the square-full numbers with Ω(n) odd. The methods used are elementary.
Extension factor: Definition, properties and problems. Part 2
Original research paper. Pages 31–39
Krassimir T. Atanassov and József Sándor
Full paper (PDF, 168 Kb) | Abstract
Some new properties of the arithmetic function called “Extension Factor” and introduced in Part 1 are studied.
A parametrised family of Mordell curves with a rational point of order 3
Original research paper. Pages 40–44
Ajai Choudhry and Arman Shamsi Zargar
Full paper (PDF, 115 Kb) | Abstract
An elliptic curve defined by an equation of the type y2 = x3 + d is called a Mordell curve. This paper is concerned with Mordell curves for which d = k2; k ∈ ℤ; k ≠ 1. The point (0, k) on such curves is of order 3 and the torsion subgroup of the group of rational points on such Mordell curves is necessarily ℤ/3ℤ. We obtain a parametrised family of Mordell curves y2 = x3 + k2 such that the rank of each member of the family is at least 3. Some elliptic curves of the family have ranks 4 and 5.
t-cobalancing numbers and t-cobalancers
Original research paper. Pages 45–58
Ahmet Tekcan and Alper Erdem
Full paper (PDF, 217 Kb) | Abstract
In this work, we determine the general terms of t-cobalancers, t-cobalancing numbers and Lucas t-cobalancing numbers by solving the Pell equation 2x2 − y2 = 2t2 − 1 for some fixed integer t ≥ 1.
Classical pairs in Zn
Original research paper. Pages 59–69
Tekuri Chalapathi, Shaik Sajana and Dasari Bharathi
Full paper (PDF, 716 Kb) | Abstract
The interplay between algebraic structures and their elements have been the most famous and productive area of the algebraic theory of numbers. Generally, the greatest common divisor and least common multiple of any two positive integers are dependably non-zero elements. In this paper, we introduce a new pair of elements, called classical pair in the ring Zn whose least common multiple is zero and concentrate the properties of these pairs. We establish a formula for determining the number of classical pairs in Zn for various values of n. Further, we present an algorithm for determining all these pairs in Zn.
A bound of sums with convolutions of Dirichlet characters
Original research paper. Pages 70–74
Teerapat Srichan
Full paper (PDF, 157 Kb) | Abstract
We use the exponent pair to bound sums
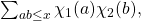
where
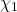
and
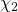
are primitive Dirichlet characters with conductors
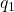
and
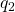
, respectively.
A new class of q-Hermite-based Apostol-type polynomials and its applications
Original research paper. Pages 75–85
Waseem A. Khan and Divesh Srivastava
Full paper (PDF, 196 Kb) | Abstract
The present article is to introduce a new class of q-Hermite based Apostol-type polynomials and to investigate their properties and characteristics. In particular, the generating functions, series expression and explicit and recurrence relations for these polynomials are established. We derive some relationships for q-Hermite based Apostol-type polynomials associated with q-Apostol-type Bernoulli polynomials, q-Apostol-type Euler and q-Apostol-type Genocchi polynomials.
A note on identities in two variables for a class of monoids
Original research paper. Pages 86–92
Enrique Salcido and Emil Daniel Schwab
Full paper (PDF, 178 Kb) | Abstract
In this note we consider identities in the alphabet X = {x, y}. This note is self-contained and the aim is to describe gradually the identities partition (with three parameters) of the free semigroup X+ for the class of monoids Bn = {a, b | ba = bn} (n > 0).
Bi-unitary multiperfect numbers, I
Original research paper. Pages 93–171
Pentti Haukkanen and Varanasi Sitaramaiah
Full paper (PDF, 432 Kb) | Abstract
A divisor d of a positive integer n is called a unitary divisor if gcd(d, n/d) = 1; and d is called a bi-unitary divisor of n if the greatest common unitary divisor of d and n/d is unity. The concept of a bi-unitary divisor is due to D. Surynarayana [12]. Let σ∗∗(n) denote the sum of the bi-unitary divisors of n. A positive integer n is called a bi-unitary perfect number if σ∗∗(n) = 2n. This concept was introduced by C. R. Wall in 1972 [15], and he proved that there are only three bi-unitary perfect numbers, namely 6, 60 and 90.
In 1987, Peter Hagis [6] introduced the notion of bi-unitary multi k-perfect numbers as solutions n of the equation σ∗∗(n) = kn. A bi-unitary multi 3-perfect number is called a bi-unitary triperfect number. A bi-unitary multiperfect number means a bi-unitary multi k-perfect number with k ≥ 3. Hagis [6] proved that there are no odd bi-unitary multiperfect numbers. We aim to publish a series of papers on bi-unitary multiperfect numbers focusing on multiperfect numbers of the form n = 2au, where u is odd. In this paper–part I of the series–we investigate bi-unitary triperfect numbers of the form n = 2au, where 1 ≤ a ≤ 3. It appears that n = 120 = 2315 is the only such number. Hagis [6] found by computer the bi-unitary multiperfect numbers less than 107. We have found 31 such numbers up to 8.1010. The first 13 are due to Hagis. After completing this paper we noticed that further numbers are already listed in The On-Line Encyclopedia of Integer Sequences (sequence A189000 Bi-unitary multiperfect numbers). The numbers listed there have been found by direct computer calculations. Our purpose is to present a mathematical search and treatment of bi-unitary multiperfect numbers.
Phidias numbers as a basis for Fibonacci analogues
Original research paper. Pages 172–178
P. S. Kosobutskyy
Full paper (PDF, 452 Kb) | Abstract
In this paper it is shown that there is a plurality of irrational values of the roots of a quadratic equation with equal modulus coefficients |p| = |q| ≠ 1 having properties of the numbers of Phidias φ = 0.61803… and Ф = 1.61803… It is shown that it is also possible to construct a set of sequences possessing the basic properties of the Fibonacci and Lucas sequences.
On the Generalized Fibonacci-circulant-Hurwitz numbers
Original research paper. Pages 179–190
Ömür Deveci, Zafer Adıgüzel and Taha Doğan
Full paper (PDF, 182 Kb) | Abstract
The theory of Fibonacci-circulant numbers was introduced by Deveci et al. In this paper, we define the Fibonacci-circulant-Hurwitz sequence of the second kind by Hurwitz matrix of the generating function of the Fibonacci-circulant sequence of the second kind and give a fair generalization of the sequence defined, which we call the generalized Fibonacci-circulant-Hurwitz sequence. First, we derive relationships between the generalized Fibonacci-circulant-Hurwitz numbers and the generating matrices for these numbers. Also, we give miscellaneous properties of the generalized Fibonacci-circulant-Hurwitz numbers such as the Binet formula, the combinatorial, permanental, determinantal representations, the generating function, the exponential representation and the sums.
On hyper-dual generalized Fibonacci numbers
Original research paper. Pages 191–198
Neşe Ömür and Sibel Koparal
Full paper (PDF, 163 Kb) | Abstract
In this paper, we define hyper-dual generalized Fibonacci numbers. We give the Binet formulae, the generating functions and some basic identities for these numbers.
Some binomial-sum identities for the generalized bi-periodic Fibonacci sequences
Original research paper. Pages 199–208
Ho-Hon Leung
Full paper (PDF, 164 Kb) | Abstract
A bi-periodic sequence is a sequence which satisfies different recurrence relations depending on whether the n-th term considered is odd or even. In this paper, we investigate the properties of the generalized bi-periodic Fibonacci sequences. It is a generalization of the biperiodic Fibonacci sequences defined by Edson and Yayenie. We derive binomial-sum identities for the generalized bi-periodic Fibonacci sequences by matrix method. Our identities generalize binomial-sum identities derived by Edson and Yayenie for the case of bi-periodic Fibonacci sequences.
Identities on the product of Jacobsthal-like and Jacobsthal–Lucas numbers
Original research paper. Pages 209–215
Apisit Pakapongpun
Full paper (PDF, 142 Kb) | Abstract
The purpose of this paper is to find the identities of Jacobsthal-like and Jacobsthal–Lucas numbers by using Binet’s formula.
Some properties of (p, q)-Fibonacci-like and (p, q)-Lucas numbers
Original research paper. Pages 216–224
Boonyen Thongkam, Khuanphirom Butsuwan and Phonpriya Bunya
Full paper (PDF, 144 Kb) | Abstract
In this paper, we present the investigation of products of (p, q)-Fibonacci-like and (p, q)-Lucas numbers. It also reveals some properties on the products of (p, q)-Fibonacci like and (p, q)-Lucas numbers.
Gaussian binomial coefficients
Original research paper. Pages 225–229
A. G. Shannon
Full paper (PDF, 523 Kb) | Abstract
This paper extends Gaussian binomial coefficients (and so-called) Fibonomial coefficients) with identities related to Horadam’s generalized binomial coefficients.
Corrigendum to “On the Iyengar–Madhava Rao–Nanjundiah inequality and its hyperbolic version” [Notes on Number Theory and Discrete Mathematics, Vol. 24, 2018, No. 2, 134–139]
Corrigendum. Page 230
József Sándor
Corrigendum (PDF, 270 Kb)
This issue of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP1-15/2019.
Volume 26 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4


