Volume 26 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
In Memoriam: Prof. Varanasi Sitaramaiah
Editorial. Page 1
Editorial (PDF, 79 Kb)
Bi-unitary multiperfect numbers, IV(a)
Original research paper. Pages 2–32
Pentti Haukkanen and Varanasi Sitaramaiah
Full paper (PDF, 320 Kb) | Abstract
On the quantity m2 − pk where pkm2 is an odd perfect number
Original research paper. Pages 33–38
Jose Arnaldo Bebita Dris and Immanuel Tobias San Diego
Full paper (PDF, 193 Kb) | Abstract
We prove that
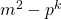
is not a square, if
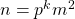
is an odd perfect number with special prime
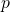
, under the hypothesis that
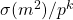
is a square. We are also able to prove the same assertion without this hypothesis. We also show that this hypothesis is incompatible with the set of assumptions
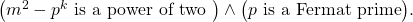
We end by stating some conjectures.
Congruences involving alternating sums related to harmonic numbers and binomial coefficients
Original research paper. Pages 39–51
Laid Elkhiri, Miloud Mihoubi and Abdellah Derbal
Full paper (PDF, 187 Kb) | Abstract
In 2017, Bing He investigated arithmetic properties to obtain various basic congruences modulo a prime for several alternating sums involving harmonic numbers and binomial coefficients. In this paper we study how we can obtain more congruences modulo a power of a prime number
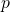
(super congruences) in the ring of
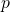
-integer
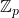
involving binomial coefficients and generalized harmonic numbers.
On a sum involving the number of distinct prime factors function related to the integer part function
Original research paper. Pages 52–56
Mihoub Bouderbala and Meselem Karras
Full paper (PDF, 146 Kb) | Abstract
In this paper, we obtain asymptotic formula on the sum
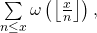
where
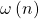
denote the number of distinct prime divisors of

and
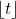
denotes the integer part of
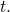
Objects generated by an arbitrary natural number
Original research paper. Pages 57–62
Krassimir Atanassov
Full paper (PDF, 158 Kb) | Abstract
The set Set(n), generated by an arbitrary natural number n, is defined. Some arithmetic functions, defined over its elements are introduced. Some of the arithmetic, set-theoretical and algebraic properties of the new objects are studied.
On Pythagorean triplet semigroups
Original research paper. Pages 63–67
Antoine Mhanna
Full paper (PDF, 142 Kb) | Abstract
In this note we explain the two pseudo-Frobenius numbers for
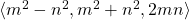
where
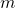
and

are two coprime numbers of different parity. This lets us give an Apéry set for these numerical semigroups.
On a translated sum over primitive sequences related to a conjecture of Erdős
Original research paper. Pages 68–73
Nadir Rezzoug, Ilias Laib and Guenda Kenza
Full paper (PDF, 220 Kb) | Abstract
For
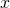
large enough, there exists a primitive sequence
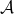
, such that
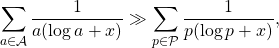
where 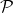 denotes the set of prime numbers.
denotes the set of prime numbers.
A study on some identities involving (sk, t)-Jacobsthal numbers
Original research paper. Pages 74–79
Serpil Halici and Mine Uysal
Full paper (PDF, 159 Kb) | Abstract
In this study, we examined the generalization of Pakapongpun for Jacobsthal numbers. With respect to this generalization, we have given some known basic identities, which have an important place in the literature.
The translated Whitney–Lah numbers: generalizations and q-analogues
Original research paper. Pages 80–92
Mahid M. Mangontarum
Full paper (PDF, 203 Kb) | Abstract
In this paper, we derive some combinatorial formulas for the translated Whitney–Lah numbers which are found to be generalizations of already-existing identities of the classical Lah numbers, including the well-known Qi’s formula. Moreover, we obtain q-analogues of the said formulas and identities by establishing similar properties for the translated q-Whitney numbers.
Explicit formula of a new class of q-Hermite-based Apostol-type polynomials and generalization
Original research paper. Pages 93–102
Mouloud Goubi
Full paper (PDF, 215 Kb) | Abstract
The present article deals with a recent study of a new class of q-Hermite-based Apostol-type polynomials introduced by Waseem A. Khan and Divesh Srivastava. We give their explicit formula and study a generalized class depending in any q-analog generating function.
A note on the Fermat quartic 34x4 + y4 = z4
Original research paper. Pages 103–105
Gustaf Söderlund
Full paper (PDF, 129 Kb) | Abstract
We show that the only primitive non-zero integer solutions to the Fermat quartic
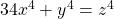
are
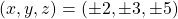
. The proofs are based on a previously given complete solution to another Fermat quartic namely
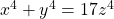
.
On a generalization of the Monkey and Coconuts Problem
Original research paper. Pages 106–112
Amitabha Tripathi
Full paper (PDF, 189 Kb) | Abstract
The original version of the Monkey and Coconuts Problem describes a hypothetical situation where five sailors and a monkey are trapped on an island and plan on equally sharing coconuts. The number of coconuts turns out to be one more than a multiple of 5. The first sailor tosses one coconut to the monkey, and then takes his equal share out of the pile. Each subsequent sailor finds the number of remaining coconuts to be one more than a multiple of 5, and repeats this process one at a time. After the last sailor has tossed one coconut to the monkey, he too takes his share. The number of coconuts that remain at this stage is a multiple of 5, and is shared equally by the five sailors. In a variation of the original problem, the number of coconuts that remain after the fifth sailor has had his share is again one more than a multiple of 5. Therefore, one coconut is again tossed to the monkey before the remaining pile can be equally distributed among the five sailors. The problem is to determine the least number of coconuts, and the final
share for each sailor in each version.
We find explicit solutions for both the original version and the variation in the general case of n sailors in which at each stage r coconuts are tossed to the monkey. Even more generally, we also investigate the two versions when the n sailors leave r1, …, rn coconuts to the monkey.
On algorithms for computing the sums of powers of arithmetic progressions
Original research paper. Pages 113–121
Peter J. Shiue, Shen C. Huang and Eric Jameson
Full paper (PDF, 164 Kb) | Abstract
This paper is concerned with sums of powers of arithmetic progressions of the form
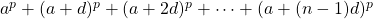
, where
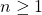
,
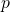
is a non-negative integer, and

and
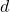
are complex numbers with
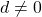
. This paper gives an elementary proof to a theorem presented by Laissaoui and Rahmani [9] as well as an algorithm based on their formula. Additionally, this paper presents a simplification to Laissaoui and Rahmani’s formula that is better suited to computation, and a second algorithm based on this simplification. Both formulas use Stirling numbers of the second kind, which are the number of ways to partition
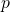
labelled objects into
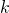
nonempty unlabelled subsets [4]. An analysis of both algorithms is presented to show the theoretical time complexities. Finally, this paper conducts experiments with varying values of
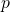
. The experimental results show the proposed algorithm remains around
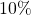
faster as
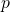
increases.
The Gauss product and Raabe’s integral for k-gamma functions
Original research paper. Pages 122–127
József Sándor
Full paper (PDF, 239 Kb) | Abstract
We obtain an extension of the famous Gauss product formula to the case of k-gamma functions. The Sándor–Tóth short product formula [16] is also attended to these functions. An asymptotic formula and Raabe’s integral analogue are also considered.
Derangement polynomials with a complex variable
Original research paper. Pages 128–135
Abdelkader Benyattou
Full paper (PDF, 170 Kb) | Abstract
In this paper, we define new polynomials with a complex variable related to the derangement polynomials and we give some properties of those polynomials. We use umbral calculus to establish a new congruence concerning the derangement polynomials with a complex variable.
Properties of hyperbolic generalized Pell numbers
Original research paper. Pages 136–153
Yüksel Soykan and Melih Göcen
Full paper (PDF, 219 Kb) | Abstract
In this paper, we introduce the generalized hyperbolic Pell numbers over the bidimensional Clifford algebra of hyperbolic numbers. As special cases, we deal with hyperbolic Pell and hyperbolic Pell–Lucas numbers. We present Binet’s formulas, generating functions and the summation formulas for these numbers. Moreover, we give Catalan’s, Cassini’s, d’Ocagne’s, Gelin–Cesàro’s, Melham’s identities and present matrices related to these sequences.
Padovan sequence generalization – a study of matrix and generating function
Original research paper. Pages 154–163
Renata Passos Machado Vieira, Francisco Regis Vieira Alves and Paula Maria Machado Cruz Catarino
Full paper (PDF, 183 Kb) | Abstract
The Padovan sequence is a sequence similar to the Fibonacci sequence, the former being third order and the latter second. Having several applications in architecture, these numbers are directly related to plastic numbers. In this paper, the Padovan sequence is studied and investigated from the standpoint of linear algebra. With this, we will study the matrix and the generating function of the extensions of this sequence (Tridovan and Tetradovan), thus determining the generalization of this sequence.
New Tribonacci recurrence relations and addition formulas
Original research paper. Pages 164–172
Kunle Adegoke, Adenike Olatinwo and Winning Oyekanmi
Full paper (PDF, 133 Kb) | Abstract
Only one three-term recurrence relation, namely,
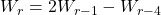
, is known for the generalized Tribonacci numbers,
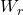
,
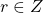
, defined by
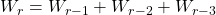
and
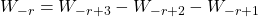
, where
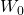
,
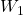
and
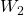
are given, arbitrary integers, not all zero. Also, only one four-term addition formula is known for these numbers, which is
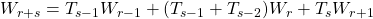
, where
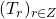
is the Tribonacci sequence, a special case of the generalized Tribonacci sequence, with
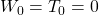
and
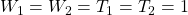
. In this paper we discover three new three-term recurrence relations and two identities from which a plethora of new addition formulas for the generalized Tribonacci numbers may be discovered. We obtain a simple relation connecting the Tribonacci numbers and the Tribonacci–Lucas numbers. Finally, we derive quadratic and cubic recurrence relations for the generalized Tribonacci numbers.
On the generalized Fibonacci and Lucas 2k−ions
Original research paper. Pages 173–186
Sure Köme and Hafize Kirik
Full paper (PDF, 288 Kb) | Abstract
This study introduces the modified generalized Fibonacci and Lucas 2k−ions which are the generalizations of several quaternions, octonions and higher order dimensional algebras. We give the generating functions, the Binet formulas and well-known identities such as Catalan’s identity and Cassini’s identity for the modified generalized Fibonacci and Lucas 2k−ions.
Dual bicomplex Horadam quaternions
Original research paper. Pages 187–205
Kübra Gül
Full paper (PDF, 220 Kb) | Abstract
The aim of this work is to introduce a generalization of dual quaternions called dual bicomplex Horadam quaternions and to present some properties, the Binet’s formula, Catalan’s identity, Cassini’s identity and the summation formula for this type of bicomplex quaternions. Furthermore, several identities for dual bicomplex Fibonacci quaternions are given.
A note on the coefficient array of a generalized Fibonacci polynomial
Original research paper. Pages 206–212
A. G. Shannon and Ömür Deveci
Full paper (PDF, 118 Kb) | Abstract
A particular version of a Fibonacci polynomial is presented and the coefficients are tabulated to bring out some of their number theory properties with known results. Generalizations of the fundamental and primordial Lucas sequences are used in the proofs
Significant role of the specific prime number p = 257 in the improvement of cryptosystems
Original research paper. Pages 213–222
Hana Ali-Pacha, Naima Hadj-Said, Adda Ali-Pacha and Özen Özer
Full paper (PDF, 118 Kb) | Abstract
Cryptology is the significant science which is inseparable from the means of communication of secrets. In a safe manner, it has the main objective of transmitting (potentially sensitive) information between two interlocutors. One distinguishes mainly two “dual” disciplines within cryptology:
(a) cryptography, which is interested in the security of information.
(b) cryptanalysis, which seeks to attack it.
One have a starting set of 256 elements, we add a new element to this set to form a set of 257 elements. In this paper, we consider a finite field that contains 257 elements. As with any field, a finite field is a set on which the operations of multiplication, addition, subtraction and division are defined and satisfy certain basic rules. The most common examples of finite fields are given by the integers modulo p when p is a prime number. For our case ℤ/pℤ, p = 257. We apply it to affine ciphers and show that this cipher looks like a permutation cipher. The idea based on this result, is to use the affine ciphers with the modulo 257 (as an initial permutation) in any specific algorithm of ciphering. Besides, one finishes with the decryption affine with the modulo 257 like an inverse permutation. This is to significantly increase the security of the specific encryption algorithm and to lengthen the 16-bits encryption key.
This issue of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP1-15/2019.
Volume 26 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
![]() , where
, where ![]() and
and ![]() is odd. There exist exactly ten such numbers. In this part we solve partly the case
is odd. There exist exactly ten such numbers. In this part we solve partly the case ![]() . We prove that if
. We prove that if ![]() is a bi-unitary triperfect number of the form
is a bi-unitary triperfect number of the form ![]() , where
, where ![]() , then
, then ![]() . We then confine ourselves to the case
. We then confine ourselves to the case ![]() . We prove that in this case we have
. We prove that in this case we have ![]() and further show that
and further show that ![]() is the only bi-unitary triperfect number of this form.
is the only bi-unitary triperfect number of this form.![]()
![]() denotes the set of prime numbers.
denotes the set of prime numbers.

