Antoine Mhanna
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367-8275
Volume 26, 2020, Number 4, Pages 63–67
DOI: 10.7546/nntdm.2020.26.4.63-67
Full paper (PDF, 156 Kb)
Details
Authors and affiliations
Antoine Mhanna ![]()
SRS College Kleiat Lebanon
Abstract
In this note we explain the two pseudo-Frobenius numbers for ![]() where
where ![]() and
and ![]() are two coprime numbers of different parity. This lets us give an Apéry set for these numerical semigroups.
are two coprime numbers of different parity. This lets us give an Apéry set for these numerical semigroups.
Keywords
- Numerical semigroups
- Primitive Pythagorean triplets
- Pseudo-Frobenius number
2010 Mathematics Subject Classification
- 11D07
- 11D45
- 11D85
- 20M14
References
- Fel, L. G. (2006). Frobenius Problem for Semigroups
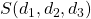 , Funct. Anal. Other Math., 1, 119–157.
, Funct. Anal. Other Math., 1, 119–157.
- Fröberg, R., Gottlieb, C., & Hägkvist, R. (1987). On numerical semigroups, Semigroup Forum, 35, 63–83.
- Gil, B. K., Han, J.-W., Kim, T. H., Koo, R. H., Lee, B. W., Lee, J., Nam, K. S., Park, H. W., & Park P.-S. (2015). Frobenius numbers of Pythagorean triples, Int. J. Number Theory, 11,613–619.
- Johnson, S. M. (1960). A Linear Diophantine Problem, Can. J. Math., 12(2), 390–398.
- Ramı́rez Alfonsı́n, J. L. (2005). The Diophantine Frobenius Problem, Oxford Univ. Press, Oxford.
- Rosales, J. C., & Branco, M. B. (2011). The Frobenius problem for numerical semigroups, Journal of Number Theory, 131, 2310–2319.
- Rosales, J. C., & Garcı́a-Sánchez, P. A. (2004). Numerical semigroups with embedding dimension three, Archiv der Mathematik, 83, 488–496.
- Rosales, J. C., & Garcı́a-Sánchez, P. A. (2009). Numerical semigroups, Springer, New York.
- Tripathi, A., & Elizeche, E. F. (2020). On numerical semigroups generated by primitive Pythagorean triplets, Integers, 20, A75
Related papers
Cite this paper
Mhanna, A. (2020). On Pythagorean triplet semigroups. Notes on Number Theory and Discrete Mathematics, 26 (4), 63-67, DOI: 10.7546/nntdm.2020.26.4.63-67.


