Volume 25, 2019, Number 4

Volume 25 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4

An asymptotic formula for the Chebyshev theta function
Original research paper. Pages 1–7
Aditya Ghosh
Full paper (PDF, 182 Kb) | Abstract

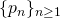
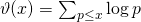
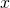
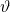
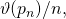
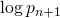
Let $\{p_n\}_{n\ge 1}$ be the sequence of primes and $\vartheta(x) = \sum_{p \leq x} \log p$ , where $p$ runs over the primes not exceeding $x$ , be the Chebyshev $\vartheta$ -function. In this note, we derive lower and upper bounds for $\vartheta(p_n)/n,$ by comparing it with $\log p_{n+1}$ and deduce the asymptotic formula $\vartheta(p_n)/n=\log p_{n+1}\left(1-\frac{1}{\log n}+\frac{\log\log n}{\log^2 n}\left(1+o(1)\right)\right).$

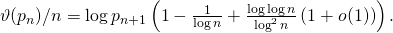
A note on balanced numbers
Original research paper. Pages 8–15
József Sándor and Krassimir T. Atanassov
Full paper (PDF, 198 Kb) | Abstract

A new proof of solvability of equations

$\frac{\sigma(n)}{d(n)} = \frac{n}{2}$

and

$\frac{\sigma_k(n)}{d(n)} = \frac{n^k}{2},$

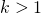for $k >1$ are given. Connections with related problems and inequalities are pointed out, too.

Certain generating functions for the quadruple hypergeometric series K₁₀
Original research paper. Pages 16–23
Praveen Agarwal, Jihad A. Younis and Taekyun Kim
Full paper (PDF, 179 Kb) | Abstract

In this work we aim at establishing certain generating relations, involving the Exton function of four variables K₁₀. Some special cases of the main results here are also considered.

A family of elliptic curves of rank ≥ 5 over ℚ(m)
Original research paper. Pages 24–29
Arman Shamsi Zargar and Naser Zamani
Full paper (PDF, 172 Kb) | Abstract

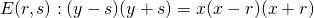
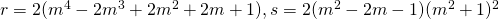
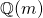
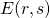
We construct a subfamily of elliptic curves $E(r,s):(y-s)(y+s)=x(x-r)(x+r)$ with $r=2(m^4-2m^3+2m^2+2m+1), s=2(m^2-2m-1)(m^2+1)^2$ , and show that its rank is at least five over $\Bbb Q(m)$ . This improves the previous results on the rank of the curves $E(r,s)$ over $\Bbb Q(m)$ .

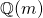
Some studies on Eisenstein series and their applications
Original research paper. Pages 30–43
H. C. Vidya and B. R. Srivatsa Kumar
Full paper (PDF, 219 Kb) | Abstract

In the present paper, we discuss some results on Eisenstein series of level 4 and 8. Also, as an application of this, we construct certain differential equations, incomplete integrals and deduce approximation to 3 / π and convolution sums.

Formal power series in several variables
Original research paper. Pages 44–57
Pentti Haukkanen
Full paper (PDF, 219 Kb) | Abstract

We present the theory of formal power series in several variables in an elementary way. This is a generalization of Niven’s theory of formal power series in one variable. We refer to a formal power series in n variables as an n-way array of complex or real numbers and investigate its algebraic properties without analytic tools. We also consider the formal derivative, logarithm and exponential of a formal power series in n variables. Applications to multiplicative arithmetical functions in several variables and cumulants in statistics are presented.

Differential and difference polynomial sequences
Original research paper. Pages 58–65
Veasna Kim, Vichian Laohakosol and Supawadee Prugsapitak
Full paper (PDF, 201 Kb) | Abstract

A polynomial sequence is a sequence of n positive integers which represents the values of an integer polynomial at the first n positive integers. We extend this notion to differential and difference polynomial sequences which are defined analogously by incorporating not only the polynomial values but also the values of its derivatives and/or differences at integer points. Characterizations and their algebraic structures are determined.

Multisection of series
Original research paper. Pages 66–71
A. G. Shannon
Full paper (PDF, 151 Kb) | Abstract

This paper extends some ideas of Leonard Carlitz with ideas from John Riordan and validated against results of Alwyn Horadam. They involve breaking up series and considering multiple sums of ordinary and generalized binomial coefficients.

Distribution of constant terms of irreducible polynomials in ℤ_p[x]
Original research paper. Pages 72–82
Sarah C. Cobb, Michelle L. Knox, Marcos Lopez, Terry McDonald and Patrick Mitchell
Full paper (PDF, 206 Kb) | Abstract

We obtain explicit formulas for the number of monic irreducible polynomials with prescribed constant term and degree q^k over a finite field. These formulas are derived from work done by Yucas. We show that the number of polynomials of a given constant term depends only on whether the constant term is a residue in the underlying field. We further show that as k becomes large, the proportion of irreducible polynomials having each constant term is asymptotically equal.

Determinants of Toeplitz–Hessenberg matrices with generalized Fibonacci entries
Original research paper. Pages 83–95
Taras Goy and Mark Shattuck
Full paper (PDF, 209 Kb) | Abstract

In this paper, we evaluate several families of Toeplitz–Hessenberg matrices whose entries are generalized Fibonacci numbers. In particular, we find simple formulas for several determinants whose entries are translates of the Chebyshev polynomials of the second kind. Equivalently, these determinant formulas may also be rewritten as identities involving sums of products of generalized Fibonacci numbers and multinomial coefficients. Combinatorial proofs which make use of sign-reversing involutions and the definition of a determinant as a signed sum over the symmetric group S_n are given for our formulas in several particular cases, including those involving the Chebyshev polynomials.

On the sum of three arbitrary Fibonacci and Lucas numbers
Original research paper. Pages 96–101
Nurettin Irmak, Zafer Şiar and Refik Keskin
Full paper (PDF, 135 Kb) | Abstract

In this paper, we solve the equations

$L_k = F_n + F_m + F_r,$

$F_k = F_n + F_m + F_r,$

$L_k = L_n + L_m + L_r,$

$F_k = L_n + L_m + L_r$

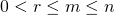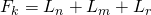for $0 < r \leq m \leq n$ and a natural number $k$ . It is shown that only the equation $F_k = L_n + L_m + L_r$ has a finite number of solutions. The others have infinitely many solutions.

s-th power of Fibonacci number of the form 2^a + 3^b + 5^c
Original research paper. Pages 102–109
Nurettin Irmak and Bo He
Full paper (PDF, 235 Kb) | Abstract

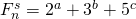
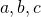
In this paper, we solve the Diophantine equation $F_{n}^{s}=2^{a}+3^{b}+5^{c}$ , where $a,b,c$ and $s$ are positive integers with $1\le \max \left\{a,b\right\} \leq c.$

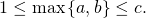
Generalized Fibonacci and k-Pell matrix sequences: Another way of demonstrating their properties
Original research paper. Pages 110–122
Francisco Regis Vieira Alves and Paula Maria Machado Cruz Catarino
Full paper (PDF, 239 Kb) | Abstract

Recently Wani, Artaf, A., Badshah, V., Rathore, G. P. & Catarino introduced
commutative matrices derived from the generalized Fibonacci matrix sequence and the k-Pell matrix sequence. In the present work, through the identification of certain special matrices, we can identify other forms of demonstration and also the description of commutative matrix properties for negative indices.

On generalized bicomplex k-Fibonacci numbers
Original research paper. Pages 123–133
Tülay Yağmur
Full paper (PDF, 166 Kb) | Abstract

In this paper, we introduce the generalized bicomplex k-Fibonacci numbers. We also give the generating function and Binet’s formula for these numbers. In addition, we obtain some identities such as Honsberger, d’Ocagne’s, Catalan’s, and Cassini’s identities involving the generalized bicomplex k-Fibonacci numbers.

An application of exponential sums over the divisor function
Original research paper. Pages 134–142
Tippawan Puttasontiphot
Full paper (PDF, 167 Kb) | Abstract

We apply the rational exponential sums over the divisor function to estimate the average of some arithmetic functions. The method of proof relies on the classic Abel’s summation formula.

On bipartite graphs and the Fibonacci numbers
Original research paper. Pages 143–149
Fatih Yılmaz and Pınar Eldutar
Full paper (PDF, 157 Kb) | Abstract

In this short note, we consider adjacency matrices of ladder graphs. Then we obtain permanental polynomials, eigenvalues and some other properties of adjacency matrix of the graph.

On Beck’s zero-divisor graph
Original research paper. Pages 150–157
Deepa Sinha and Bableen Kaur
Full paper (PDF, 154 Kb) | Abstract

For a commutative ring R with unity (1 ≠ 0), the zero-divisor graph of R, denoted by Γ(R), is a simple graph with vertices as elements of R and two distinct vertices are adjacent whenever the product of the vertices is zero. This article aims at gaining a deeper insight into the basic structural properties of zero-divisor graphs given by Beck.

This issue of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP-28/2018.

Volume 25 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4

Latest Issue

Journal Contents