Determinants of Toeplitz–Hessenberg matrices with generalized Fibonacci entries

Taras Goy and Mark Shattuck
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 25, 2019, Number 4, Pages 83-95
DOI: 10.7546/nntdm.2019.25.4.83-95
Full paper (PDF, 219 Kb)

Details

Authors and affiliations

Taras Goy
Faculty of Mathematics and Computer Science
Vasyl Stefanyk Precarpathian National University
57 Shevchenko St., 76018 Ivano-Frankivsk, Ukraine

Mark Shattuck
Department of Mathematics, University of Tennessee
37996 Knoxville, TN, USA

Abstract

In this paper, we evaluate several families of Toeplitz–Hessenberg matrices whose entries are generalized Fibonacci numbers. In particular, we find simple formulas for several determinants whose entries are translates of the Chebyshev polynomials of the second kind. Equivalently, these determinant formulas may also be rewritten as identities involving sums of products of generalized Fibonacci numbers and multinomial coefficients. Combinatorial proofs which make use of sign-reversing involutions and the definition of a determinant as a signed sum over the symmetric group S_n are given for our formulas in several particular cases, including those involving the Chebyshev polynomials.

Keywords

• Toeplitz–Hessenberg matrix
• Horadam sequence
• Trudi’s formula
• Generating function
• Chebyshev polynomials

2010 Mathematics Subject Classification

• 11B39
• 05A15
• 15B05

References

1. Benjamin, A. T. & Quinn, J. J. (2003).Proofs that Really Count: The Art of Combinatorial Proof, Mathematical Association of America, Washington, DC.
2. Cereceda, J. L. (2014). Determinantal representations for generalized Fibonacci and Tribonacci numbers, International Journal of Contemporary Mathematical Sciences, 9 (6), 269–285.
3. Goy, T. (2018). Horadam sequence through recurrent determinants of tridiagonal matrix, Kragujevac Journal of Mathematics, 42 (4), 527–532.
4. Goy, T. (2019). On some combinatorial identities involving the Horadam numbers, Abstractsof XII International Algebraic Conference in Ukraine, 2–6 July 2019, Vinnytsia, Ukraine, 37–38.
5. Horadam, A. F. (1965). Basic properties of a certain generalized sequence of numbers, Fibonacci Quarterly, 3 (2), 161–176.
6. Horadam, A. F. (1967). Special properties of the sequence 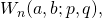Fibonacci Quarterly, 5 (5), 424–434.
7. Horadam, A. F. (1969). Tschebyscheff and other functions associated with the sequence 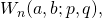Fibonacci Quarterly, 7 (1), 14–22.
8. Ipek, A. (2011). On the determinants of pentadiagonal matrices with the classical Fibonacci, generalized Fibonacci and Lucas numbers, Eurasian Mathematical Journal, 2 (2), 60–74.
9. Larcombe, P. J. (2017). Horadam sequences: a survey update and extension,Bulletin of the Institute of Combinatorics and its Applications, 80, 99–118.
10. Mason, J. C. & Handscomb, D. C. (2002). Chebyshev Polynomials, Chapman and Hall/CRC, Boca Raton.
11. Merca, M. (2013). A note on the determinant of a Toeplitz–Hessenberg matrix, Special Matrices, 1, 10–16.
12. Muir, T. (1960).The Theory of Determinants in the Historical Order of Development, Vol. 3,Dover Publications, New York.
13. Shen, S.-Q. & Liu, W.-J. (2016). Inversion of lower Hessenberg matrix involving classical Horadam numbers, International Journal of Algebra, 10 (7), 343–350.
14. Tangboonduangjit, A. & Thanatipanonda, T. (2016). Determinants containing powers of generalized Fibonacci numbers, Journal of Integer Sequences, 19, Article 16.7.1.