Volume 25 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
The linear combination of two triangular numbers is a perfect square
Original research paper. Pages 1–12
Junyao Peng
Full paper (PDF, 187 Kb) | Abstract
By the basic properties of Pell equation and the theory of congruence, we investigate the problem about the linear combination of two triangular numbers is a perfect square. First, we show that if 2
n is not a perfect square, the Diophantine equation
![Rendered by QuickLaTeX.com \[1+n\binom y 2=z^2\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-cbe979e4412f2853c927be4f954a1150_l3.png)
has infinitely many positive integer solutions (y,z). Second, we prove that if m,n are some special values, the Diophantine equation
![Rendered by QuickLaTeX.com \[m\binom x 2+n\binom y 2=z^2\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-c1bc088e6f390f206a17367d13d5fa4f_l3.png)
Composition of happy functions
Original research paper. Pages 13–20
Passawan Noppakeaw, Niphawan Phoopha and Prapanpong Pongsriiam
Full paper (PDF, 193 Kb) | Abstract
Direct parametrization of Pythagorean triples
Original research paper. Pages 21–35
Sungkon Chang
Full paper (PDF, 240 Kb) | Abstract
If the two axes of symmetry of a quadratic form in two variables have integer coefficients, the reflection across the axes defines a group action on the primitive solutions of the Diophantine equation defined by the quadratic form. In this paper, we introduce quadratic forms with rational axes of symmetry that admit a single set of polynomials which parametrize their primitive solutions up to the reflections.
Extension factor: definition, properties and problems. Part 1
Original research paper. Pages 36–43
Krassimir T. Atanassov and József Sándor
Full paper (PDF, 166 Kb) | Abstract
A new arithmetic function, called “Extension Factor” is introduced and some of its properties are studied.
Numbers with the same kernel
Original research paper. Pages 44–64
Rafael Jakimczuk
Full paper (PDF, 241 Kb) | Abstract
In this article we study functions related to numbers which have the same kernel. We apply the results obtained to the sums
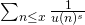
, where
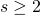
is an arbitrary but fixed positive integer and
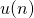
denotes the kernel of

. For example, we prove that
![Rendered by QuickLaTeX.com \[\sum_{n\leq x}\frac{1}{u(n)^s}\sim f_{s}(x), \]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-e1e524524379298eec042c18b436858c_l3.png)
where
![Rendered by QuickLaTeX.com \[f_{s}(x)=\sum^{\infty}_{k=1}\frac{b_{k,s}}{k!}(\log x)^k\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-84ab1ae2c77178467751970bc6503ec9_l3.png)
and the positive coefficients 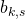 of the series have a strong connection with the prime numbers. We also prove that
of the series have a strong connection with the prime numbers. We also prove that
![Rendered by QuickLaTeX.com \[\sum_{n\leq x}\frac{1}{u(n)^s}=\exp\left(\left(\log x\right)^{\beta_s(x)}\right), \]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-33740a6f699a4a11f70db73df22d3e1d_l3.png)
where 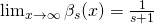 . The methods used are very elementary. The case
. The methods used are very elementary. The case  , namely
, namely  , was studied, as it is well-known, by N. G. de Bruijn (1962) and W. Schwarz (1965).
, was studied, as it is well-known, by N. G. de Bruijn (1962) and W. Schwarz (1965).
On ternary biquadratic Diophantine equation 11(x2 – y2) + 3(x + y ) =10z4
Original research paper. Pages 65–71
S. Vidhyalakshmi, M. A. Gopalan , S. A. Thangam and Ö. Özer
Full paper (PDF, 91 Kb) | Abstract
We obtain infinitely many non-zero integer triples (x, y, z) satisfying the non-homogeneous bi-quadratic equation with three unknowns 11(x 2 – y 2) + 3(x + y ) =10 z 4. Various interesting properties among the values of x, y, z are presented. Some relations between the solutions and special numbers are exhibited.
On applications of blending generating functions of q-Apostol-type polynomials
Original research paper. Pages 72–86
Ugur Duran, Mehmet Acikgoz and Serkan Araci
Full paper (PDF, 217 Kb) | Abstract
Motivated by Kurt’s blending generating functions of q-Apostol polynomials [16], we investigate some new identities and relations. We also aim to derive several new connections between these polynomials and generalized q-Stirling numbers of the second kind. Additionally, by making use of the fermionic p-adic integral over the p-adic numbers field, some relationships including unified Apostol-type q-polynomials and classical Euler numbers are obtained.
Gaussian Mersenne numbers and generalized Mersenne quaternions
Original research paper. Pages 87–96
Ahmet Daşdemir and Göksal Bilgici
Full paper (PDF, 156 Kb) | Abstract
In this study, we introduce a new class of quaternions associated with the well-known Mersenne numbers. There are many studies about the quaternions with special integer sequences and their generalizations. All of these studies used consecutive elements of the considered sequences. Here, we extend the usual definitions into a wider structure by using arbitrary Mersenne numbers. Moreover, we present Gaussian Mersenne numbers. In addition, we give some properties of this type of quaternions and Gaussian Mersenne numbers, including generating function and Binet-like formula.
A note on generalized Leonardo numbers
Original research paper. Pages 97–101
A. G. Shannon
Full paper (PDF, 98 Kb) | Abstract
This is essentially an expository paper which sheds new light on existing knowledge due to Asveld and Horadam and suggests ideas for extension and generalization based on the approaches of these authors.
Sum formulas involving powers of balancing and Lucas-balancing numbers – II
Original research paper. Pages 102–110
S. G. Rayaguru and G. K. Panda
Full paper (PDF, 146 Kb) | Abstract
In this paper, we derive expressions for the sums of first four powers of balancing and Lucas-balancing numbers by using the telescoping summation formula. Further, we use these new results to obtain other closed form expressions studied earlier.
Dual-complex k-Pell quaternions
Original research paper. Pages 111–125
Fügen Torunbalcı Aydın
Full paper (PDF, 200 Kb) | Abstract
In this paper, dual-complex k-Pell numbers and dual-complex k-Pell quaternions are defined. Also, some algebraic properties of dual-complex k-Pell numbers and quaternions which are connected with dual-complex numbers and k-Pell numbers are investigated. Furthermore, Honsberger Identity, d’Ocagne’s Identity, Binet’s Formula, Cassini’s Identity and Catalan’s Identity for these quaternions are given.
On bicomplex numbers with coefficients from the complex Fibonacci sequence
Original research paper. Pages 126–137
Serpil Halıcı and Şule Çürük
Full paper (PDF, 182 Kb) | Abstract
The aim of this paper is to introduce a new sequence of bicomplex numberswith coefficients from the complex Fibonacci sequence, and to investigate some fundamen-
tal properties of the newly defined sequence.
A remark on the Tribonacci sequences
Original research paper. Pages 138–141
Lilija Atanassova
Full paper (PDF, 110 Kb) | Abstract
One of the first extensions of the Fibonacci sequence are the Tribonacci sequences. In the paper, some of their properties are discussed.
Convolution identities for Tetranacci numbers
Original research paper. Pages 142–169
Takao Komatsu and Rusen Li
Full paper (PDF, 245 Kb) | Abstract
Convolution identities for various numbers (e.g., Bernoulli, Euler, Genocchi, Catalan, Cauchy and Stirling numbers) have been studied by many authors. Recently, several convolution identities have been studied for Fibonacci and Tribonacci numbers too. In this paper, we give convolution identities with and without binomial (multinomial) coefficients for Tetranacci numbers, and convolution identities with binomial coefficients for Tetranacci and Tetranacci-type numbers.
Close encounters of the golden and silver ratios
Original research paper. Pages 170–184
Robin James Spivey
Full paper (PDF, 233 Kb) | Abstract
What are the nearest approaches of the natural powers of two irrational numbers, allowing for arbitrarily large exponents? In the case of the first two metallic means, a definitive answer to this challenging question lies within reach. Despite the small magnitude of the golden ratio,
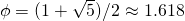
, and the silver ratio,
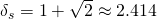
, the integers approximated by their powers, namely the Lucas (
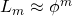
) and Pell-Lucas (
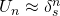
) numbers, never coincide except in trivial cases for which
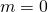
. The equation
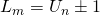
has only four solutions for
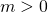
,
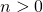
. The largest such encounter arises between
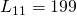
and
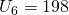
whilst the separation between larger pairings,
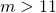
and
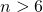
, always exceeds 42.
Sequences of Tridovan and their identities
Original research paper. Pages 185–197
Renata Passos Machado Vieira, and Francisco Regis Vieira Alves
Full paper (PDF, 197 Kb) | Abstract
This work introduces the so-called Tridovan sequence which is an extended form of the Padovan sequence. In a general definition, this extension adds one more term to the Padovan recurrence relation, considering now the three terms preceding the penultimate one. Studies carried out on the proposed extension reveal properties of the positive and negative integer index, the sum of all, even and odd terms, the obtaining Tridovan Q-matrix and finally the Tridovan initial terms generalization.
On the software computation of the formulae for the n-th prime number
Original research paper. Pages 198–206
Dimitar G. Dimitrov
Full paper (PDF, 188 Kb) | Abstract
Many formulae for calculating the n-th prime number exist. In this paper, a comparison of the computation time of different existing formulae is made.
On the distribution of k-free numbers and r-tuples of k-free numbers. A survey
Survey paper. Pages 207–222
Radoslav Tsvetkov
Full paper (PDF, 226 Kb) | Abstract
This paper presents a brief survey of the current state of the distribution of k-free numbers and r-tuples of k-free numbers. We state the main problems in the field, sketch their history and the basic machinery used to study them.
This issue of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP-28/2018.
Volume 25 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
![]()
![]()
![]()
![]() is the expansion of
is the expansion of ![]() in base
in base ![]() . We call
. We call ![]() an
an ![]() -happy function. Let
-happy function. Let ![]() be a composition of various
be a composition of various ![]() -happy functions. We show that, for any given
-happy functions. We show that, for any given ![]() , the iteration sequence
, the iteration sequence ![]() either converges to a fixed point or eventually becomes a cycle. Here
either converges to a fixed point or eventually becomes a cycle. Here ![]() is the identity function mapping
is the identity function mapping ![]() to
to ![]() for all
for all ![]() and
and ![]() is the
is the ![]() -fold composition of
-fold composition of ![]() . In addition, we prove that the number of all possible fixed points and cycles is finite. Examples are also given.
. In addition, we prove that the number of all possible fixed points and cycles is finite. Examples are also given.![]()
![Rendered by QuickLaTeX.com \[f_{s}(x)=\sum^{\infty}_{k=1}\frac{b_{k,s}}{k!}(\log x)^k\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-84ab1ae2c77178467751970bc6503ec9_l3.png)
![]() of the series have a strong connection with the prime numbers. We also prove that
of the series have a strong connection with the prime numbers. We also prove that![]()
![]() . The methods used are very elementary. The case
. The methods used are very elementary. The case ![]() , namely
, namely ![]() , was studied, as it is well-known, by N. G. de Bruijn (1962) and W. Schwarz (1965).
, was studied, as it is well-known, by N. G. de Bruijn (1962) and W. Schwarz (1965).

