Volume 20, 2014, Number 3

It follows from our previous works and those of Nathanson that if P is a set of primes, then the greater the cardinality of P, the less likely that there exists a sequence of polynomials, satisfying the functional equation arising from multiplication of quantum integers studied by Nathanson, which has P as its support base and which cannot be generated by quantum integers. In this paper we analyze the set of roots of the polynomials involved leading to a direct construction of a polynomial solution Γ which has infinite support base P and which cannot be generated by quantum integers. Our results demonstrate that there are more to these solutions than those provided by quantum integers. In addition, we also show that a result of Nathanson does not hold if the condition t_Γ = 1 is removed.

Recently, I. Gueye proved a variant of Clement’s Theorem on twin primes. We show that, this result follows by a simple identity.

Let N(x) be the number of perfect powers that do not exceed x. In this note we obtain asymptotic formulae for the difference N(x + x^θ) − N(x), where 1/2 < θ < 2/3 + 1/7. We also prove that if θ = 1/2 the difference N(x + x^θ) − N(x) is zero for infinite x arbitrarily large.

Summation of certain infinite series involving powers of square root of natural numbers is evaluated through Riemann zeta function. The sum of powers of square root of first n natural numbers are expressed in terms of infinite series and Riemann zeta function.

If we use the expression F_p = kp ± 1, p prime, then digital sums of k reveal specific values for primes versus composites in the range 7 ≤ p ≤ 107. The associated digital sums of F_p±1 also yield prime/composite specificity. It is shown too that the first digit of F_p, and hence for the corresponding triples, (F_p, F_p±1) and (F_p, F_p−1, F_p−2) can be significant for primality checks.

The inequality

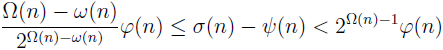
connecting φ, ψ and σ-functions is formulated and proved.

A new characterization of 2m-prime pairs is obtained. In particular, twin prime pairs are characterized. Our results give elementary methods for finding 2m-prime pairs (e.g. twin prime pairs) up to a given integer.

In this paper the s_k–Jacobsthal numbers are introduced and their properties are studied.

The General Euclidean Algorithm (GEA) is the natural generalization of the Euclidean Algorithm (EA) and equivalent to Semi Regular Continued Fractions (SRCF). In this paper, we consider the finite case with entries in GEA natural numbers. Consider the Euclidean Division. In GEA we want the divider to be bigger than the absolute value of the remainder. Thus, we take two divisions except for the case the remainder is zero. However, for our help, we consider the non Euclidean remainder without the negative sign so as not to take the absolute value of it for the next step of the algorithm as we need to have two positive integers. So, it occurs a binary tree except for the before last vertex of its path which gives one division as the remainder is zero. This paper presents mainly a criterion with which we can find all the shortest paths of this tree and not only the one that Valhen–Kronecker’s criterion gives. In terms of SRCF, this criterion gives all the SRCF expansions of a rational number t with the same length as the Nearest Integer Continued Fraction (NICF) expansion of t. This criterion, as we shall see, is related to the golden ration. 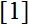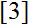Afterwards, it is presented a theorem which connects the Fibonacci sequence with the difference between the longest and the shortest path of this tree, a theorem which connects the Fibonacci sequence with the longest path of this tree and a different proof of a theorem which occurs by and which connects the Pell numbers with the shortest path of the aforementioned tree. After that, it is proven a connection of this tree to the harmonic and the geometric mean and in particular two new criteria of finding a shortest path are constructed based on this two means. 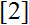In the final chapter, it is an algorithm, which has an “opposite” property of the EA, property which has been proven in and has to do with the number of steps Least Remainder Algorithm (LRA) needs to be finished in relation to EA and the signs of the remainders of LRA path.