Volume 24 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Some formulae which match with the prime counting function infinitely often
Original research paper. Pages 1–4
Yannick Saouter
Full paper (PDF, 157 Kb) | Abstract
Recently K. Gaitanas gave a formula which matches with the counting prime function for an infinite set of values of its argument. In this note, we give a construction of an infinite number of such formulae.
On Dris conjecture about odd perfect numbers
Original research paper. Pages 5–9
Paolo Starni
Full paper (PDF, 141 Kb) | Abstract
The Euler’s form of odd perfect numbers, if any, is n = παN2, where π is prime, (π, N) = 1 and π ≡ α ≡ 1 (mod 4). Dris conjecture states that N > πα. We find that N2 > 1/2 πγ, with γ = max{ω(n) − 1, α}; ω(n) ≥ 10 is the number of distinct prime factors of n.
An indicator characteristic for twin prime formation independent of integer size
Original research paper. Pages 10–15
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 199 Kb) | Abstract
The modular ring Z6 has twin primes located in the same row. This enables the structural mechanisms underlying the formation of twin primes to be summarised by simple equations. The classification system provided by right-end-digits applies equally in all integer domains of any size, and can be used to demonstrate the formation of twin primes in such domains.
On a generalization of Eulerian numbers
Original research paper. Pages 16–42
Claudio Pita-Ruiz
Full paper (PDF, 261 Kb) | Abstract
We consider the sequence
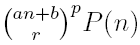
, product of the
rp-th degree
n-polynomial
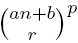
, where
a,
b ∈ ℂ,
a ≠ 0,
r,
p ∈ ℕ, and the
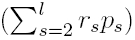
-th degree n-polynomial
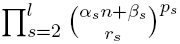
, where
αs,
βs ∈ ℂ,
rs,
ps ∈ ℕ,
s = 2, …,
l. In the expansion of the polynomial
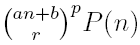
in terms of the binomials
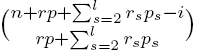
,
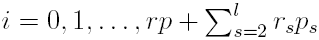
, the resulting coefficients
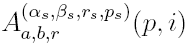
are the generalized Eulerian numbers we consider in this work (the case
P(
n) = 1,
a = 1,
b = 0
, r = 1 corresponds to the standard Eulerian numbers). We obtain results on symmetries, recurrences, row sums, and alternating row sums, that generalize the corresponding well-known results for the standard Eulerian numbers. The main tool we use to obtain our results throughout the work, is the Z-transform of sequences.
Proofs of certain conjectures for means of two arguments
Original research paper. Pages 43–48
József Sándor
Full paper (PDF, 150 Kb) | Abstract
We offer proofs of certain inequalities for means conjectured by N. Elezovic [2].
A new proof of Euler’s pentagonal number theorem
Original research paper. Pages 49–52
A. David Christopher
Full paper (PDF, 163 Kb) | Abstract
A new proof of Euler’s pentagonal number theorem is obtained.
New index matrix representations of operations over natural numbers
Original research paper. Pages 53–60
Lilija Atanassova
Full paper (PDF, 166 Kb) | Abstract
Two new operations over index matrices are introduced. Their possible application in number theory is discussed and illustrated with examples related to the canonical representation of the natural numbers and with two extended Fibonacci sequences.
Almost arithmetic progressions in ℤ/pℤ
Original research paper. Pages 61–75
Mario Huicochea
Full paper (PDF, 202 Kb) | Abstract
For k ∈ ℕ ∪ {0} and r ∈ ℤ/pℤ \ {0}, we say that a subset X of ℤ/pℤ is a k-almost arithmetic progression with difference r if there is an arithmetic progression Y with difference r containing X such that |Y\X| ≤ k. Let X be a k-almost arithmetic progression with difference r such that k + 2 < |X| < p − 4k − 9. The main result of this paper is following: if there is t ∈ ℤ/pℤ \ {0} such that X is also a k-almost arithmetic progression with difference t, then t ∈ {±r}. Moreover, we will show that our result is sharp.
Fourier series of sums of products of Bernoulli and Euler/Genocchi functions
Original research paper. Pages 76–93
Taekyun Kim, Dae San Kim, Toufik Mansour and Gwan-Woo Jang
Full paper (PDF, 282 Kb) | Abstract
We study the Fourier series of functions related to sum of products of Bernoulli polynomials and either Euler or Genocchi polynomials. As consequences, several new identities for the Bernoulli, Euler, and Genocchi functions and numbers are derived.
Short note on a new arithmetic function
Original research paper. Pages 94–96
Krassimir T. Atanassov
Full paper (PDF, 136 Kb) | Abstract
A new arithmetic function is introduced. It is illustrated with some examples with well known arithmetic functions, as, e.g., π– and φ-functions.
The greatest common divisors of generalized Fibonacci and generalized Pell numbers
Original research paper. Pages 97–102
Boonyen Thongkam and Nutcha Sailadda
Full paper (PDF, 141 Kb) | Abstract
Abd-Elhameed and Zeyada have introduced the generalized sequence of numbers (Una,b,r)n≥0 such that sequence generalizes both generalized Fibonacci numbers (Gna,b)n≥0 and generalized Pell numbers (Pna,b)n≥0. In the present paper, we show a study of the greatest common divisors of some Gna,b, Pna,b and Una,b,r.
Fibonacci and Lucas numbers via the determinants of tridiagonal matrix
Original research paper. Pages 103–108
Taras Goy
Full paper (PDF, 167 Kb) | Abstract
Applying the apparatus of triangular matrices, we proved new recurrence formulas for the Fibonacci and Lucas numbers with even (odd) indices by tridiagonal determinants.
The arrowhead-Pell-random-type sequences
Original research paper. Pages 109–119
Özgür Erdağ, Anthony G. Shannon and Ömür Deveci
Full paper (PDF, 210 Kb) | Abstract
In this paper, we define the arrowhead-Pell-random-type sequence and then we obtain the generating function and the generating matrix of the sequence. Also, we derive the permanental, determinantal, combinatorial and exponential representations and the sums of the arrowhead-Pell-random-type numbers using the generating function and the generating matrix of the sequence.
On generalizations of the Jacobsthal sequence
Original research paper. Pages 120–135
Fügen Torunbalcı Aydın
Full paper (PDF, 227 Kb) | Abstract
In this paper, the generalized Jacobsthal and generalized complex Jacobsthal and generalized dual Jacobsthal sequences using the Jacobsthal numbers are investigated. Also, special cases of these sequences are investigated. Furthermore, recurrence relations, vectors, the golden ratio and Binet’s formula for the generalized Jacobsthal sequences and generalized dual Jacobsthal sequences are given.
Corrigendum to “Sum of dilates of two sets” [Notes on Number Theory and Discrete Mathematics, Vol. 23, 2017, No. 4, 34–41]
Corrigendum. Page 136
Raj Kumar Mistri
Corrigendum (PDF, 47 Kb)
This issue of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. DNP-06-38/2017.
Volume 24 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
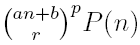 , product of the rp-th degree n-polynomial
, product of the rp-th degree n-polynomial 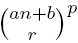 , where a, b ∈ ℂ, a ≠ 0, r, p ∈ ℕ, and the
, where a, b ∈ ℂ, a ≠ 0, r, p ∈ ℕ, and the 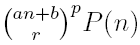 in terms of the binomials
in terms of the binomials 

