Volume 23 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
On a curious biconditional involving the divisors of odd perfect numbers
Original research paper. Pages 1–13
Jose Arnaldo B. Dris
Full paper (PDF, 177 Kb) | Abstract
We investigate the implications of a curious biconditional involving the divisors of odd perfect numbers, if Dris conjecture that qk < n holds, where qkn2 is an odd perfect number with Euler prime q. We then show that this biconditional holds unconditionally. Lastly, we prove that the inequality q < n holds unconditionally.
Short remark on a special numerical sequence
Original research paper. Pages 14–17
Krassimir T. Atanassov
Full paper (PDF, 152 Kb) | Abstract
The sequence G = {2233…pnpn}n ≥ 1 is discussed and some of its properties are studied.
A note on bounds for the Neuman–Sándor mean using power and identric means
Original research paper. Pages 18–21
József Sándor
Full paper (PDF, 127 Kb) | Abstract
In this note we point out priority results and new proofs related to the bounds for the Neuman–Sándor mean in terms of the power means and the identric means.
Prime triples p1, p2, p3 in arithmetic progressions such that p1 = x2 + y2 + 1, p3 = [nc]
Original research paper. Pages 22–33
S. I. Dimitrov
Full paper (PDF, 225 Kb) | Abstract
In the present paper we prove that there exist infinitely many arithmetic progressions of three different primes
p1,
p2,
p3 = 2
p2 −
p1 such that
p1 =
x2 +
y2 + 1,
p3 =
 nc
nc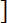
.
Sum of dilates of two sets
Original research paper. Pages 34–41
Raj Kumar Mistri
Full paper (PDF, 151Kb) | Abstract
Let A⊆ Z and B ⊆ Z be nonempty finite sets and let r be a nonzero integer. The sumof dilates of A and B is defined as A + r · B := {a + rb : a ∈ A and b ∈ B}. Finding nontriviallower bound for the sum of dilates is an important problem in additive combinatorics and it hasapplications in sum-product problems. In case of A = B, a recent result of Freiman et al. states that if r ≥ 3, then |A + r · A| ≥ 4|A| – 4. We generalize this result for the sum of dilates A + r · B for two sets A and B, where r is an integer with |r| ≥ 3.
On limits and formulae where functions of slow increase appear
Original research paper. Pages 42–51
Rafael Jakimczuk
Full paper (PDF, 168 Kb) | Abstract
Let An be a strictly increasing sequence of positive integers such that An ∼ nsf(n), where f(x) is a function of slow increase and s is a positive real number. In this article we obtain some limits and asymptotic formulae where appear functions of slow increase. As example, we apply the obtained results to the sequence of numbers with exactly k prime factors in their prime factorization, in particular to the sequence of prime numbers (k = 1).
Two applications of the Hadamard integral inequality
Original research paper. Pages 52–55
József Sándor
Full paper (PDF, 127 Kb) | Abstract
As applications of the Hadamard integral inequality, we offer two inequalities for trigonometric, resp. hyperbolic functions. One of results gives a new proof of the Iyengar–Madhava Rao–Nanjundiah inequality for (sin x / x).
Some properties of the bi-periodic Horadam sequences
Original research paper. Pages 56–65
Elif Tan
Full paper (PDF, 168 Kb) | Abstract
In this paper, we give some basic properties of the bi-periodic Horadam sequences which generalize the known results for the bi-periodic Fibonacci and Lucas sequences. Also, we obtain some new identities for the bi-periodic Lucas sequences.
Generalized dual Pell quaternions
Original research paper. Pages 66–84
Fügen Torunbalcı Aydın, Kevser Köklü and Salim Yüce
Full paper (PDF, 228 Kb) | Abstract
In this paper, we defined the generalized dual Pell quaternions. Also, we investigated the relations between the generalized dual Pell quaternions. Furthermore, we gave the Binet’s formulas and Cassini-like identities for these quaternions.
Some variations on Fibonacci matrix graphs
Original research paper. Pages 85–93
Anthony G. Shannon and Ömür Deveci
Full paper (PDF, 105 Kb) | Abstract
Matrices are here considered in two ways: arrays containing Fibonacci numbers and their generalizations in the cells, and arrays as graphs where the cells themselves are subgraphs. Both aspects contain ideas for further development and research.
Volume 23 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4


