Volume 23 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
On the extensibility of the 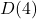 -triple
-triple 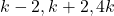 over Gaussian integers
over Gaussian integers
Original research paper. Pages 1–26
Abdelmejid Bayad, Appolinaire Dossavi-Yovo, Alan Filipin, and Alain Togbé
Full paper (PDF, 246 Kb) | Abstract
In this paper, we prove that if
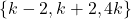
, where
![Rendered by QuickLaTeX.com k \in \mathbb{Z}[i], k \ne 0, \pm 2](https://nntdm.net/wp-content/ql-cache/quicklatex.com-7b97451666f44d2ed159e442ee9f7ad9_l3.png)
, is a
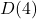
-quadruple in the ring of Gaussian integers, then
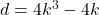
.
All associated Stirling numbers are arithmetical triangles
Original research paper. Pages 27–34
Khaled Ben Letaïef
Full paper (PDF, 176 Kb) | Abstract
Associated Stirling numbers of first and second kind are usually found in the literature in various forms of stairs depending on their order

. Yet, it is shown in this note that all of these numbers can be arranged, through a linear transformation, in the same arithmetical triangle structure as the “Pascal’s triangle”.
A short proof of a concrete sum
Original research paper. Pages 35–37
Samuel G. Moreno and Esther M. García-Caballero
Full paper (PDF, 133 Kb) | Abstract
We give an alternative proof of a formula that generalizes Hermite’s identity. Instead involving modular arithmetic, our short proof relies on the Fourier-type expansion for the floor function and on a trigonometric formula.
On k-balancing numbers
Original research paper. Pages 38–52
Arzu Özkoç and Ahmet Tekcan
Full paper (PDF, 205 Kb) | Abstract
In this work, we consider some algebraic properties of

-balancing numbers. We deduce some formulas for the greatest common divisor of

-balancing numbers, divisibility properties of

-balancing numbers, sums of

-balancing numbers and simple continued fraction expansion of

-balancing numbers.
The abundancy index of divisors of odd perfect numbers – Part III
Original research paper. Pages 53–59
Jose Arnaldo B. Dris
Full paper (PDF, 139 Kb) | Abstract
Dris gave numerical bounds for the sum of the abundancy indices of
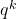
and
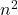
, where
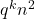
is an odd perfect number, in his master’s thesis. In this note, we show that improving the limits for this sum is equivalent to obtaining nontrivial bounds for the Euler prime
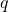
.
On a Pillai’s Conjecture and gaps between consecutive primes
Original research paper. Pages 60–72
Rafael Jakimczuk
Full paper (PDF, 199 Kb) | Abstract
In this article we show that the following Pillai’s conjecture
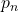
is the

-th prime number)
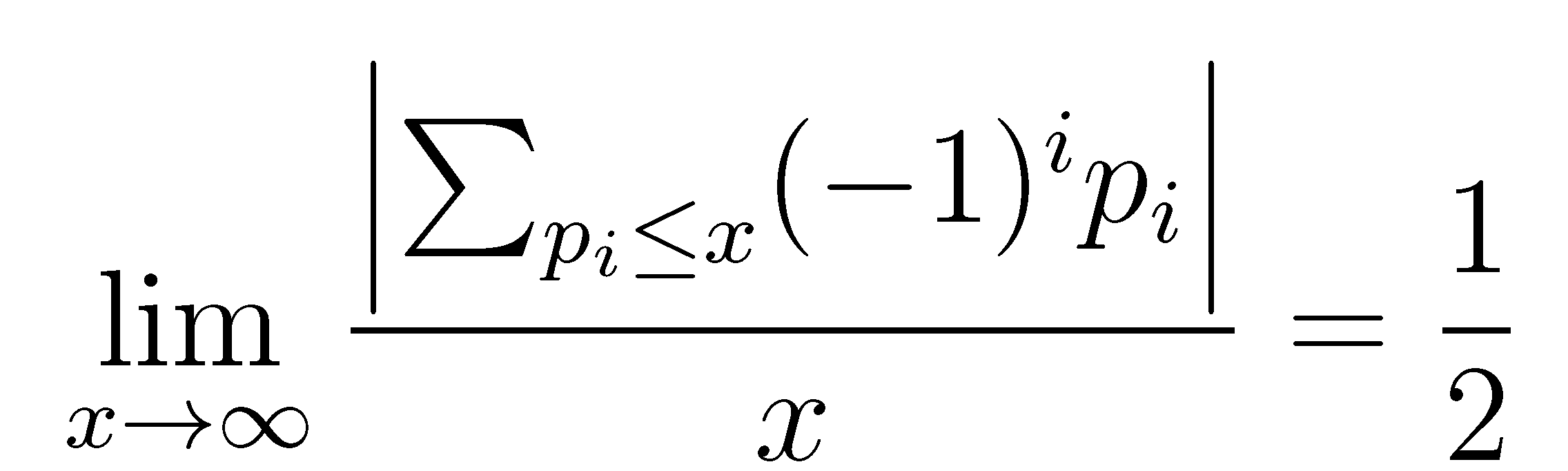
can be established in terms of gaps between consecutive primes. We also study general sequences that have this property. We call these sequences Pillai sequences. We prove that the sequence of perfect powers is a Pillai-sequence.
On quasiperfect numbers
Original research paper. Pages 73–78
V. Siva Rama Prasad and C. Sunitha
Full paper (PDF, 158 Kb) | Abstract
A natural number
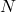
is said to be quasiperfect if
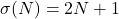
where
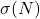
is the sum of the positive divisors of
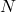
. No quasiperfect number is known. If a quasiperfect number
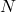
exists and if
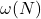
is the number of distinct prime factors of
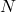
then G. L. Cohen has proved
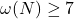
while H. L. Abbott et. al have shown
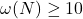
if
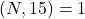
. In this paper we first prove that every quasiperfect numbers
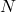
has an odd number of special factors (see definition 2.3 below) and use it to show that
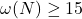
if
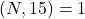
which refines the result of Abbott et.al. Also we provide an alternate proof of Cohen’s result when
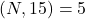
.
A Wilf class composed of 19 symmetry classes of quadruples of 4-letter patterns
Original research paper. Pages 79–99
Talha Arıkan, Emrah Kılıç and Toufik Mansour
Full paper (PDF, 240 Kb) | Abstract
In this paper, we make a contribution to the enumeration of permutations avoiding a quadruples of 4-letter patterns by establishing a Wilf class composed of 19 symmetry classes.
Pell–Padovan-circulant sequences and their applications
Original research paper. Pages 100–114
Ömür Deveci and Anthony G. Shannon
Full paper (PDF, 315 Kb) | Abstract
This paper develops properties of recurrence sequences defined from circulant matrices obtained from the characteristic polynomial of the Pell-Padovan sequence. The study of these sequences modulo m yields cyclic groups and semigroups from the generating matrices. Finally, we obtain the lengths of the periods of the extended sequences in the extended triangle groups
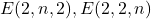
and
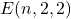
for
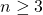
as applications of the results obtained.
On two new two-dimensional extensions of the Fibonacci sequence
Original research paper. Pages 115–122
Krassimir T. Atanassov
Full paper (PDF, 133 Kb) | Abstract
Two new two-dimensional extensions of the Fibonacci sequence are introduced. Explicit formulas for their

-th members are given.
Non-split domination subdivision critical graphs
Original research paper. Pages 123–132
Girish V. R. and P. Usha
Full paper (PDF, 154 Kb) | Abstract
A set of vertices S is said to dominate the graph G if for each v ∉ S, there is a vertex u ∈ S with v adjacent to u. The minimum cardinality of any dominating set is called the domination number of G and is denoted by γ(G). A dominating set D of a graph G = (V, E) is a non-split dominating set if the induced graph ⟨V – D⟩ is connected. The non-split domination number γns(G) is the minimum cardinality of a non-split domination set. The purpose of this paper is to initiate the investigation of those graphs which are critical in the following sense: A graph G is called vertex domination critical if γ(G − v) < γ(G) for every vertex v in G. A graph G is called vertex non-split critical if γns(G − v) < γns(G) for every vertex v in G. Thus, G is k–γns-critical if γns(G) = k, for each vertex v ∈ V(G), γns(G − v) < k. A graph G is called edge domination critical if (G + e) < (G) for every edge e in G. A graph G is called edge non-split critical if γns(G + e) < γns(G) for every edge e ∈ G. Thus, G is k–γns-critical if γns(G) = k, for each edge e ∈ G, γns(G + e) < k. First we have constructed a bound for a non-split domination number of a subdivision graph S(G) of some particular classes of graph in terms of vertices and edges of a graph G. Then we discuss whether these particular classes of subdivision graph S(G) are γns-critical or not with respect to vertex removal and edge addition.
Volume 23 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
![]() -triple
-triple ![]() over Gaussian integers
over Gaussian integers