On a Pillai’s Conjecture and gaps between consecutive primes

Rafael Jakimczuk
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 23, 2017, Number 3, Pages 60–72
Full paper (PDF, 199 Kb)

Details

Authors and affiliations

Rafael Jakimczuk
División Matemática, Universidad Nacional de Luján
Buenos Aires, Argentina

Abstract

In this article we show that the following Pillai’s conjecture p_n is the n-th prime number)

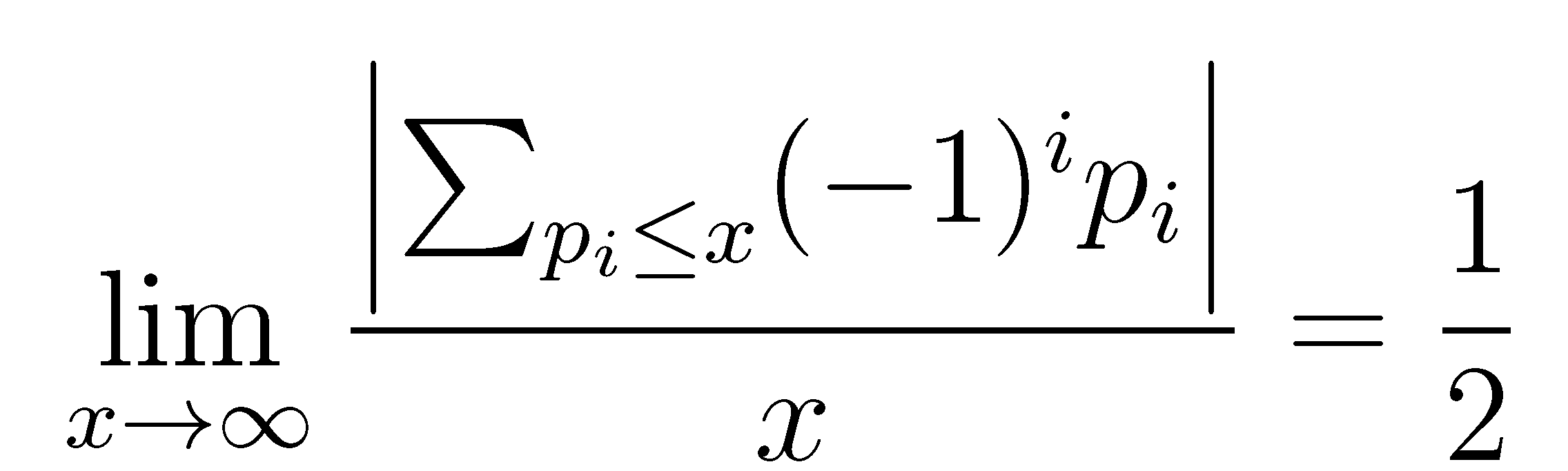
can be established in terms of gaps between consecutive primes. We also study general sequences that have this property. We call these sequences Pillai sequences. We prove that the sequence of perfect powers is a Pillai-sequence.

Keywords

• Pillai’s conjecture
• Gaps between consecutive primes
• General sequences
• Sequence of perfect powers

AMS Classification

• 11A99
• 11B99

References

1. Chowla, S. (1965) The Riemann Hypothesis and Hilbert’s Tenth Problem, Gordon andBreach, Science Publishers.
2. Jakimczuk, R. (2010) Functions of slow increase and integer sequences, Journal of Integer Sequences, 13, Article 10.1.1.
3. Jakimczuk, R. (2015) Some results of the difference between consecutive perfect powers, Gulf Journal of Mathematics, 3(3), 9–32.
4. Jakimczuk, R. (2012) Asymptotic formulae for the n-th perfect power, Journal of Integer Sequences, 15, Article 12.5.5.
5. Rey Pastor, J., Pi Calleja, P. & Trejo, C. (1969) Analisis Matematico, Editorial Kapelusz.