Volume 21 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
A natural partial order on the prime numbers
Original research paper. Pages 1–9
Lucian M. Ionescu
Full paper (PDF, 229 Kb) | Abstract
A natural partial order on the set of prime numbers was derived by the author from the internal symmetries of the primary finite fields
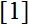
, independently of
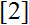
, who investigated Pratt trees
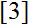
used for primality tests. It leads to a correspondence with the Hopf algebra of rooted trees, and as an application, to an alternative approach to the Prime Number Theorem.
A note on the Lebesgue–Radon–Nikodym theorem with respect to weighted and twisted p-adic invariant integral on ℤp
Original research paper. Pages 10–17
Joo-Hee Jeong, Jin-Woo Park, Seog-Hoon Rim and Joung-Hee Jin
Full paper (PDF, 184 Kb) | Abstract
In this paper we will give the Lebesgue–Radon–Nikodym theorem with respect to weighted and twisted p-adic q-measure on ℤp. In special case, if there is no twisted, then we can derive the same result as Jeong and Rim, 2012; If the case weight zero and no twist, then we derive the same result as Kim 2012.
Distribution of prime numbers by the modified chi-square function
Original research paper. Pages 18–30
Daniele Lattanzi
Full paper (PDF, 246 Kb) | Abstract
The statistical distribution of prime numbers represents an open problem in number theory still nowadays. The methodology of experimental mathematics has not yet been attempted in this field, thus the present report treats prime numbers as raw experimental data and as elements of larger and larger finite sequences {Pm}. The modified chi-square function Χ2k(A, x/μ) with the ad-hoc A, k and μ = μ(k) parameters is the best-fit function of the differential distribution functions of both prime finite sequences {Pm} and truncated progressions {nα} with α ∈ (1, 2) so that an injective map can be set between them through the parameter k of their common fit function Χ2k(A, x/μ) showing that the property of scale invariance does not hold for prime distribution. The histograms of prime gaps, which are best fitted by standard statistical distribution functions, show unexpected clustering effects.
A basic logarithmic inequality, and the logarithmic mean
Original research paper. Pages 31–35
József Sándor
Full paper (PDF, 146 Kb) | Abstract
By using the basic logarithmic inequality ln x ≤ �x − 1 we deduce integral inequalities, which particularly imply the inequalities G < L < A for the geometric, logarithmic, resp. arithmetic means.
Evaluationally relatively prime polynomials
Original research paper. Pages 36–41
Michelle L. Knox, Terry McDonald and Patrick Mitchell
Full paper (PDF, 154 Kb) | Abstract
Two polynomials from
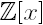
are called evaluationally relatively prime if the greatest common divisor of the two polynomials in
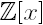
is 1 and gcd(
f(
t);
g(
t)) = 1 for all t ∈ ℤ: A characterization is given for when a linear function is evaluationally relatively prime with another polynomial.
On some Pascal’s like triangles. Part 8
Original research paper. Pages 42–50
Krassimir T. Atanassov
Full paper (PDF, 159 Kb) | Abstract
In a series of papers, Pascal’s like triangles with different forms have been described. Here, three-dimensional analogues of these triangles are given and some of their properties are studied.
An infinite primality conjecture for prime-subscripted Fibonacci numbers
Original research paper. Pages 51–55
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 129 Kb) | Abstract
The row structures of the prime-subscripted Fibonacci numbers in the modular ring Z4 show distinction between primes and composites. The class structure of the Fibonacci numbers suggest that these row structures must survive to infinity and hence that Fibonacci primes must too. The functions Fp = Kp ± 1 and Fp (factors) = kp ± 1 support the structural evidence. The graph of (K/k) versus p displays a Raman-spectra form persisting to infinity: ln(K/k) is linear in p in the composite case while primes lie along the p-axis to infinity.
Infinite arctangent sums involving Fibonacci and Lucas numbers
Original research paper. Pages 56–66
Kunle Adegoke
Full paper (PDF, 150 Kb) | Abstract
We derive numerous infinite arctangent summation formulas involving Fibonacci and Lucas numbers. While most of the results obtained are new, a couple of ‘celebrated’ results appear as particular cases of the more general formulas derived here.
A note on generalized Tribonacci sequence
Original research paper. Pages 67–69
Aldous Cesar F. Bueno
Full paper (PDF, 139 Kb) | Abstract
In this study, we provide a property of the generalized Tribonacci sequence through limits.
Congruent numbers via the Pell equation and its analogous counterpart
Original research paper. Pages 70–78
Farzali Izadi
Full paper (PDF, 154 Kb) | Abstract
The aim of this article is twofold. The first aim consists of introducing several polynomials of one variable as well as two variables defined on the positive integers with values as congruent numbers. The second aim is to present connections between Pythagorean triples and the Pell equation x2 − dy2 = 1 plus its analogous counterpart x2 − dy2 = − 1 which give rise to congruent numbers n with arbitrarily many prime factors.
GCED reciprocal LCEM matrices
Original research paper. Pages 79–85
Zahid Raza and Seemal Abdul Waheed
Full paper (PDF, 181 Kb) | Abstract
We have given structure theorems for a greatest common exponential divisor (GCED) and reciprocal least common exponential multiple (LCEM) matrix and calculated their determinants. The inverses and determinants of GCED and reciprocal LCEM matrices on exponential divisor closed sets have been determined.
Some identities on Schläfli-type mixed modular equations
Original research paper. Pages 86–91
B. R. Srivatsa Kumar, B. Sowmya Navada and Ranjani Nayak
Full paper (PDF, 139 Kb) | Abstract
Srinivasa Ramanujan has recorded eleven Schläfli-type mixed modular equations on p. 86 of his first notebook. Using some of these in this paper, we obtain some new identities of the same type by using Maple.
The Fascinating World of Graph Theory by Arthur Benjamin, Gary Chartrand & Ping Zhang
Book review. Page 92
A. G. Shannon
Book review (PDF, 51 Kb)
Volume 21 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4


