Volume 21 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Some Diophantine equations concerning biquadrates
Original research paper. Pages 1–5
Ajai Choudhry
Full paper (PDF, 130 Kb) | Abstract
This paper is concerned with integer solutions of the Diophantine equation x14 + x24 + x34 = k x42 where k is a given positive integer. Till now, integer and parametric solutions of this Diophantine equation have been published only when k = 1 or 2 or 3. In this paper we obtain parametric solutions of this equation for 43 values of k ≤ 100. We also show that the equation cannot have any solution in integers for 54 values of k ≤ 100. The solvability of the equation x14 + x24 + x34 = k x42 where k could not be determined for three values of k ≤ 100, namely 34, 35 and 65.
On Diophantine triples and quadruples
Original research paper. Pages 6–16
Yifan Zhang and G. Grossman
Full paper (PDF, 196 Kb) | Abstract
In this paper we consider Diophantine triples {a, b, c} (denoted D(n)-3-tuples) and give necessary and sufficient conditions for existence of integer n given the 3-tuple {a, b, c} so that ab + n, ac + n, bc + n are all squares of integers. Several examples as applications of the main results, related to both Diophantine triples and quadruples, are given.
The sum of squares for primes
Original research paper. Pages 17–21
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 87 Kb) | Abstract
Only prime integers that are in Class ̅14 of the Modular Ring Z4 equate to a sum of squares of integers x and y. A simple equation to predict these integers is developed which distinguishes prime and composite numbers in that one (x, y) couple exists for primes, but composites have either one couple with a common factor or the same number of couples as there are factors. In particular, composite Fibonacci numbers always have multiple (x, y) couples because the factors are all elements of ̅14.
Two triangular number primality tests and twin prime counting in arithmetic progressions of modulus 8
Original research paper. Pages 22–29
Werner Hürlimann
Full paper (PDF, 103 Kb) | Abstract
Two triangular number based primality tests for numbers in the arithmetic progressions 8n ± 1 are obtained. Their use yield a new Diophantine approach to the existence of an infinite number of twin primes of the form (8n−1, 8n+1).
Generating function and combinatorial proofs of Elder’s theorem
Original research paper. Pages 30–35
Robson da Silva, Jorge F. A. Lima, José Plínio O. Santos and Eduardo C. Stabel
Full paper (PDF, 208 Kb) | Abstract
We revisit Elder’s theorem on integer partitions, which is a generalization of Stanley’s theorem. Two new proofs are presented. The first proof is based on certain tilings of 1 × ∞ boards while the second one is a consequence of a more general identity we prove using generating functions.
Prime values of meromorphic functions and irreducible polynomials
Original research paper. Pages 36–39
Simon Davis
Full paper (PDF, 150 Kb) | Abstract
The existence of prime values of meromorphic functions and irreducible polynomials is considered. An argument for an infinite number of prime values of irreducible polynomials over
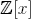
is provided.
On (M, N)-convex functions
Original research paper. Pages 40–47
József Sándor and Edith Egri
Full paper (PDF, 168 Kb) | Abstract
We consider certain properties of functions f : J → I (I, J intervals) such that f(M(x, y)) ≤ N(f(x), f(y)), where M and N are general means. Some results are extensions of the case M = N = L, where L is the logarithmic mean.
On the number of semi-primitive roots modulo n
Original research paper. Pages 48–55
Pinkimani Goswami and Madan Mohan Singh
Full paper (PDF, 176 Kb) | Abstract
Consider the multiplicative group of integers modulo n, denoted by ℤ*n. An element a ∈ ℤ*n is said to be a semi-primitive root modulo n if the order of a is φ (n)�/2, where φ�(n) is the Euler’s phi-function. In this paper, we’ll discuss on the number of semi-primitive roots of non-cyclic group ℤ*n and study the relation between S(n) and K(n), where S(n) is the set of all semi-primitive roots of non-cyclic group ℤ*n and K(n) is the set of all quadratic non-residues modulo n.
Primes within generalized Fibonacci sequences
Original research paper. Pages 56–63
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 117 Kb) | Abstract
The structure of the ‘Golden Ratio Family’ is consistent enough to permit the primality tests developed for φ5 to be applicable. Moreover, the factors of the composite numbers formed by a prime subscripted member of the sequence adhere to the same pattern as for φ5. Only restricted modular class structures allow prime subscripted members of the sequence to be a sum of squares. Furthermore, other properties of φ5 are found to apply to those other members with structural compatibility.
On some q-Pascal’s like triangles
Original research paper. Pages 64–69
Toufik Mansour and Matthias Schork
Full paper (PDF, 192 Kb) | Abstract
We consider q-analogs of Pascal’s like triangles, which were studied by Atanassov in a series of papers.
A generalization of Ivan Prodanov’s inequality
Original research paper. Pages 70–73
Krassimir T. Atanassov
Full paper (PDF, 121 Kb) | Abstract
A generalization of Prof. Ivan Prodanov’s inequality is formulated and proved. As a partial case, an inequality discussed in D. Mitrinovic and M. Popadic’s book
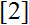
is obtained.
A generalized recurrence formula for Stirling numbers and related sequences
Original research paper. Pages 74–80
Mark Shattuck
Full paper (PDF, 157 Kb) | Abstract
In this note, we provide a combinatorial proof of a generalized recurrence formula satisfied by the Stirling numbers of the second kind. We obtain two extensions of this formula, one in terms of r-Whitney numbers and another in terms of q-Stirling numbers of Carlitz. Modifying our proof yields analogous formulas satisfied by the r-Stirling numbers of the first kind and by the r-Lah numbers.
Volume 21 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4


