Volume 8, 2002, Number 3

Volume 8 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4

About Tartaglion’s representation of planes
Original research paper. Pages 77–84
Blagoi N. Djokov
Full paper (PDF, 297 Kb) | Abstract

In the paper ℜ3 is considered, but as a special and a new commutative ring. The elements of this ring are called tartaglions. Necessary and sufficient conditions, for a plane in ℜ3 to be representated by Cartesian tartaglion’s equation, are established.

Algebraic and geometric analysis of a Fermat/Cardano cubic
Original research paper. Pages 85–94
J. V. Leyendekkers, A. G. Shannon and C. K. Wong
Full paper (PDF, 463 Kb) | Abstract

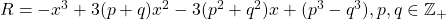
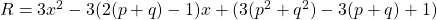
It is shown that the functions R = - x^3 + 3(p + q)x^2 - 3(p^2 + q^2)x + (p^3 - q^3), p,q \in \mathbb{Z}_+, and R = 3x^2 - 3(2(p + q ) - 1 ) x + (3(p^2 + q^2) - 3(p + q) + 1 ) intersect at a point that is always non-integer, A geometric analysis shows that the cubic crosses the x -axis at a point, x0, that is always non-integer, with x_0 = N^\frac{1}{n} (p + q + (2pq)^\frac{1}{2}), N,n \in \mathbb{Z}_+, 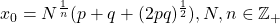where N^\frac{1}{n} 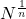is obtained from the geometry of the curve. 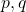These results show that a general parameter associated with the real roots of Fermat/Cardano polynomials is a function of p, q and the geometry of the curve, which in turn yield the link with the geometry of the complex plane.

Powers as a difference of squares: The effect on triples
Original research paper. Pages 95–106
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 519 Kb) | Abstract

All powers equal a difference of squares so that triples may be expressed as the sum of three squares which equal the sum of another three squares. However, when n > 2 integer values for all the components should be impossible according to the work which peaked with Wiles. By utilizing the properties of the Modular Ring ℤ4 we illustrate how the underlying Class structures of the integers justifies this constraint.

An invariant integrals in the p-adic number fields
Original research paper. Pages 107–111
Lee Chae Jang
Full paper (PDF, 174 Kb) | Abstract

In this paper we investigate some properties of non-Archimedean integration which is defined by T. Kim, cf. [2]. By using our results in this paper, we can give an answer of the problems which is remained by I.-C. Huang and S-Y. Huang in [1: p. 179].

New variant of a Fibonacci plane
Original research paper. Pages 112–115
Krassimir T. Atanassov and Anthony G. Shannon
Full paper (PDF, 110 Kb)

On a generalization of identities of Hoggatt and Horadam
Original research paper. Page 116
A. G. Shannon and J. H. Clarke
Full paper (PDF, 45 Kb)

Volume 8 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4

Comments are closed.