Volume 17 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
The relation between π(x) and certain arithmetic functions
Original research paper. Pages 1–9
Magdalena Corciovei-Bănescu
Full paper (PDF, 178 Kb) | Abstract
We prove an improvement Rosser–Schoenfeld inequalities, more precisely:
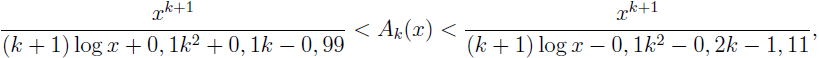
where
Ak(
x) = Σ
p ≤ x pk and
k ≥ 0.
A characterization of modularity in graphs
Original research paper. Pages 10–12
Yilun Shang
Full paper (PDF, 121 Kb) | Abstract
We present alternative expressions for modularity in graphs. Modularity is used as a measure to characterize the community of networks, which is one of the most important features in real-world networks, especially social networks.
Note on φ, ψ and σ-functions. Part 3
Original research paper. Pages 13–14
Krassimir Atanassov
Full paper (PDF, 96 Kb) | Abstract
Equalities connecting φ, ψ and σ–functions are formulated and proved.
On a class of infinite sequences with relatively prime numbers and twin prime conjecture
Original research paper. Pages 15–17
Blagoy N. Djokov
Full paper (PDF, 116 Kb) | Abstract
In this paper, a class of infinite sequences with positive integer terms is considered. If the Twin Prime Conjecture, stipulating that there are infinitely many twin prime numbers, is true, then the sequence of all twin prime numbers belongs to the same class. In the present investigation, it is proved that the mentioned class is non-empty and moreover there exists at least one element of this class containing all twin primes.
On the Diophantine equation yn = f(x)n + g(x)
Original research paper. Pages 18–21
R. Srikanth and S. Subburam
Full paper (PDF, 131 Kb) | Abstract
In this paper, we simplify the algorithm of Szalay
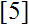
.
A note on switching in symmetric n–sigraphs
Original research paper. Pages 22–25
P. Siva Kota Reddy, B. Prashanth and Kavita S. Permi
Full paper (PDF, 138 Kb) | Abstract
In this note, we define switching in a different manner and obtained some results on symmetric n-sigraphs.
The structure of even powers in Z3: Critical structural factors that prevent the formation of even–powered triples greater than squares
Original research paper. Pages 26–30
J. V. Leyendekkers and A. Shannon
Full paper (PDF, 119 Kb) | Abstract
Integer structure analysis illustrates the critical structural factors which underpin the failure of (N4m + M4m) ever to equal an equivalent power. The number 3 plays a vital role as integers divisible by 3, when raised to an even power of the form 4m, have rows in a table of modular rings which are triangular numbers, whereas other integers raised to the same power have rows which are pentagonal numbers. The substructure within these sequences of pentagonal numbers is order within order, analogous to structure in chaos theory.
The structure of geometric number sequences
Original research paper. Pages 31–37
J. V. Leyendekkers and A. Shannon
Full paper (PDF, 50 Kb) | Abstract
An integer structure analysis (ISA) of the triangular, tetrahedral, pentagonal and pyramidal numbers is developed. The relationships among the elements and the powers of the elements of these sequences are discussed. In particular, the triangular and pentagonal numbers are directly linked and are structurally important for the formation of triples. The class structure in the modular rings Z3 and Z4 of some elements of these sequences reinforce previous studies of their properties.
Some properties and applications of a new arithmetic function in analytic number theory
Original research paper. Pages 38–48
Ramesh Kumar Muthumalai
Full paper (PDF, 189 Kb) | Abstract
We introduce an arithmetic function and study some of its properties analogous to Möbius function in analytic number theory. In addition, we derive some simple expressions to connect infinite series and infinite products through this new arithmetic function. Moreover, we study applications of this new function to derive simple identities on partition of an integer and some special infinite products in terms of multiplicative functions.
Some properties of unitary addition Cayley graphs
Original research paper. Pages 49–59
Deepa Sinha, Pravin Garg and Anjali Singh
Full paper (PDF, 180 Kb) | Abstract
Let Γ be an abelian group and B be a subset of Γ. The addition Cayley graph G′ = Cay+(Γ, B) is the graph having the vertex set V (G′) = Γ and the edge set E(G′) = {ab : a + b ∈ B}, where a, b ∈ Γ. For a positive integer n > 1, the unitary addition Cayley graph Gn is the graph whose vertex set is Zn, the integers modulo n and if Un denotes set of all units of the ring Zn, then two vertices a, b are adjacent if and only if a + b ∈ Un. The unitary addition Cayley graph Gn is also defined as, Gn = Cay+(Zn, Un). In this paper, we discuss the several properties of unitary addition Cayley graphs and also obtain the characterization of planarity and outerplanarity of unitary addition Cayley graphs.
Erratum to “Modular rings and the integer 3”
Erratum. Page 60
Erratum (PDF, 10 Kb)
Volume 17 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4


