Volume 17 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
On a limit involving the product of prime numbers
Original research paper. Pages 1–3
József Sándor and Antoine Verroken
Full paper (PDF, 142 Kb) | Abstract
Let p
k denote the
kth prime number. The aim of this note is to prove that the limit of the sequence

is
e.
Note on the matrix Fermat’s equation
Original research paper. Pages 4–11
Aleksander Grytczuk and Izabela Kurzydło
Full paper (PDF, 182 Kb) | Abstract
We consider the Fermat’s equation Xn + Yn = Zn in the set of 2 × 2 rational matrices. We give some necessary condition of solvabillity of this equation.
On some application of the spectral properties of the matrices
Original research paper. Pages 12–17
Aleksander Grytczuk and Izabela Kurzydło
Full paper (PDF, 170 Kb) | Abstract
In the paper
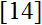
A. Schinzel and H. Zassenhaus posed the following conjecture: If
α ≠ 0 is an algebraic integer of degree n which is not a root of unity, then there exists a constant
c > 0 such that
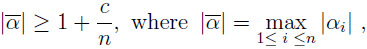
where
α =
α1; and
α2, …,
αn are the conjugates of
α.
In this paper we give some information concerning this conjecture. In the proofs of the theorems we use some spectral properties of matrices.
New results on some multiplicative functions
Original research paper. Pages 18–30
Mladen Vassilev-Missana and Peter Vassilev
Full paper (PDF, 266 Kb) | Abstract
The paper is a continuation of
. The considerations are over the class of multiplicative functions with strictly positive values and more precisely, over the pairs (
f,
g) of such functions, which have a special property, called in the paper property
S. For every such pair (
f,
g) and for every composite number
n > 1, the problem of finding the maximum and minimum of the numbers
f(
d)
g(
n/d), when
d runs over all proper divisors of n, is completely solved. Since some classical multiplicative functions like Euler’s totient function
φ, Dedekind’s function
ψ, the sum of all divisors of m, i.e.
σ(m), the number of all divisors of
m, i.e.
τ(m), and 2
ω(m) (where
ω(m) is the number of all prime divisors of m) form pairs having property
S, we apply our results to these functions and also resolve the questions of finding the maximum and minimum of the numbers
φ(d)σ(n/d),
φ(d)ψ(n/d),
τ(d)σ(n/d), 2
ω(d)σ(n/d), where
d runs over all proper divisors of
n. In addition some corollaries from the obtained results, concerning unitary proper divisors, are made. Since many other pairs of multiplicative functions (except the considered in the paper) have property
S, they may be investigated in similar manner in a future research.
On multiplicative functions with strictly positive values
Original research paper. Pages 31–36
Mladen Vassilev-Missana and Peter Vassilev
Full paper (PDF, 209 Kb) | Abstract
The paper is a continuation of
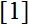
and
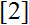
. The considerations are over the class of multiplicative functions with strictly positive values and more precisely, over the pairs (
f,
g) of such functions, which have a special property, called in the paper property
S. For every two such pairs (
f1,
g) and (
f2,
g), with different
f1 and
f2, a sufficient condition for the coincidence of the maximum (respectively of the minimum) of the numbers
f1(
d)
g(
n/
d) and
f2(
d)
g(
n/
d), where d runs over all proper divisors of an arbitrary composite number
n > 1, is given. Some applications of the results are made for several classical multiplicative functions like Euler’s totient function
φ, Dedekind’s function
ψ, the sum of all divisors of m, i.e.
σ(m), the number of all divisors of m, i.e.
τ(m), and 2
ω(m), where
ω(m) is the number of all prime divisors of
m.
Remark on Jacobsthal numbers. Part 2
Original research paper. Pages 37–39
Krassimir T. Atanassov
Full paper (PDF, 123 Kb)
Structure analysis of the perimeters of primitive Pythagorean triples
Original research paper. Pages 40–46
J. V. Leyendekkers, A. G. Shannon
Full paper (PDF, 278 Kb) | Abstract
Structural analysis (via the modular rings Z4, Z6) shows that the Perimeters, Pr, of primitive Pythagorean Triples (pPts) do not belong to simple functions. However, the factors x, (x+y) of the perimeter do, and the number of pPts in a given interval can be estimated from this. When x is prime, the series for (x+y) is complete and the associated pPts are one third of the total. When x is composite, members of the series for (x+y) are invalid when common factors with x occur. These members are not associated with pPts. When 3|(x+y), Pr ∈ ̅36, while if 3 ∤(x+y), Pr ∈ { ̅16, ̅36}. Class ̅36 dominates in the distribution.
Modular rings and the integer 3
Original research paper. Pages 47–51
J. V. Leyendekkers, A. G. Shannon
Full paper (PDF, 176 Kb) | Erratum (PDF, 10 Kb) | Abstract
The characteristics within modular rings of the integer three are discussed. This integer has unique row structures in modular rings which appear to underlie restraints on various aspects of triples, particularly the factors and powers structure of the components. The function N = xm + 2n, with m even and n odd but x not divisible by 3, always has 3 as a factor, and a majority of elements of the sequence of triangular numbers {NT} are such that 3|NT. The modular ring Z3 and the distribution of primes within its structure are also discussed.
On the classes of Steiner loops of small orders
Original research paper. Pages 52–68
M. H. Armanious
Full paper (PDF, 565 Kb) | Abstract
According to the number of sub-SL(8)s (sub-STS(7)s), there are five classes of sloops SL(16)s (STS(15)s)
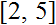
.) In
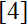
the author has classified SL(20)s into 11 classes. Using computer technique in
the authors gave a large number for each class of SL(20)s. There are only simple SL(22)s and simple SL(26)s. So the next admissible cardinality is 28. Also, all SL(32)s are classified into 14 classes in
. We try to generalize the classification of SL(20)s given in
for SL(2
n)s for each possible n and applying this method for
n = 14 to classify all possible classes of SL(28)s. Consequently, we can establish all classes of nonsimple SL(28)s and all classes of semi-planar SL(28)s (STS(27)s). In this article, we show in section 3 that there are nine classes of SL(28)s (STS(27)s having one sub-SL(14) (sub-STS(13)) and r sub-SL(8)s (sub- STS(7)s) for
r = 0, 1, 2, 3, 4, 5, 8, 11 or 16. All these sloops are subdirectly irreducible having exactly one proper homomorphic image isomorphic to SL(2). In section 4, we construct all classes of semi-planar SL(28)s. Such SL(28)s (STS(27)s) have
r sub-SL(8)s (sub-STS(7)s) for
r =1, 2, 3, 4, 5, 8, 11, 16 but no sub-SL(14) (sub-STS(13)).
In
is determined a necessary and sufficient condition for a sub-SL(2) = {1,
x} of an SL(2
n) to be normal. This result supplies us with the following two facts. First, there is another nonsimple subdirectly irreducible SL(2
n) having exactly one proper homomorphic image isomorphic to an SL(n). Accordingly, we can construct all classes of nonsimple subdirectly irreducible SL(28)s. Second fact is that if an SL(2
n) has a simple sub-SL(
n) and (
n – 1)(
n – 2)/6 sub-SL(8)s passing through a non-unit element, then SL(2
n) is isomorphic to the direct product SL(
n) × SL(2). According to the result of section 3 and the above two facts, we may say that there are 8 simple classes of SL(28)s and only 11 classes of nonsimple SL(28)s, all these classes have no sub-SL(10)s. In the last section, we construct an example for each class given above of nonmsimple and simple (semi-planar) SL(28)s (STS(27)s). Finally, we review the classes of SL(2
n)s (STS(2
n – 1)s) in 3 tables for 2
n = 16, 20, and 28.
Volume 17 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4