Graham’s number stable digits: An exact solution

Marco Ripà
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 3, Pages 607–616
DOI: 10.7546/nntdm.2025.31.3.607-616
Full paper (PDF, 1390 Kb)

Details

Authors and affiliations

Marco Ripà
Independent Researcher
Rome, Italy

Abstract

In the decimal numeral system, we prove that the well-known Graham’s number, G := \mbox{ }^{n}3 (i.e., 3^{3^{\udots^{3}}} (n times)), and any base 3 tetration whose hyperexponent is larger than n share the same \mathrm{slog}_3(G) - 1 rightmost digits (where \mathrm{slog} indicates the integer super-logarithm). This is an exact result since the \mathrm{slog}_3(G)\text{-th} rightmost digit of G differs from the \mathrm{slog}_3(G)\text{-th} rightmost digit of ^{n+1}3. Furthermore, we show that the \mathrm{slog}_3(^{n}3)\text{-th} least significant digit of the difference between Graham’s number and any base 3 tetration whose integer hyperexponent exceeds n is 4.

Keywords

  • Graham’s number
  • Tetration
  • Congruence speed
  • Power tower
  • Stable digits
  • Frozen digits
  • Powers of 3
  • Decimal system

2020 Mathematics Subject Classification

  • 11A07
  • 11F33

References

  1. Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2022). Introduction to Algorithms. (4th ed.). The MIT Press, Cambridge, Massachusetts.
  2. Exoo, G. (2003). A Euclidean Ramsey problem. Discrete & Computational Geometry, 29(2), 223–227.
  3. Gardner, M. (1977). Mathematical games. Scientific American, 237(5), 18–28.
  4. Gobel, F., & Nederpelt, R. P. (1971). The number of numerical outcomes of iterated powers. The American Mathematical Monthly, 78(10), 1097–1103.
  5. Graham, R. L., & Rothschild, B. L. (1971). Ramsey’s Theorem for n-parameter sets. Transactions of the American Mathematical Society, 159, 257–292.
  6. Guy, R. K., & Selfridge, J. L. (1973). The nesting and roosting habits of the laddered parenthesis. The American Mathematical Monthly, 80(8), 868–876.
  7. Knuth, D. E. (1976). Mathematics and computer science: Coping with finiteness. Science, 194(4271), 1235–1242.
  8. McWhirter, N. (Compiler). (1979). Guinness Book of World Records, 1980. Sterling Publishing Company, New York.
  9. OEIS Foundation Inc. (2024). A133613. The Online Encyclopedia of Integer Sequences. Available online at: https://oeis.org/A133613.
  10. Ripà, M. (2011). La Strana Coda della Serie 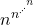n^{n^{\udots{^{^n}}}}. UNI Service, Trento, Italy.
  11. Ripà, M. (2020). On the constant congruence speed of tetration. Notes on Number Theory and Discrete Mathematics, 26(3), 245–260.
  12. Ripà, M. (2021). The congruence speed formula. Notes on Number Theory and Discrete Mathematics, 27(4), 43–61.
  13. Ripà, M. (2024). Congruence speed of the tetration bases ending with 0. Preprint. arXiv:2402.07929v1 [math.NT]. Available online at: https://arxiv.org/pdf/2402.07929.
  14. Ripà, M., & Onnis, L. (2022). Number of stable digits of any integer tetration.  Notes on Number Theory and Discrete Mathematics, 28(3), 441–457.
  15. Surhone, L. M., Timpledon, M. T., & Marseken, S. F. (2010). Super-Logarithm: Mathematics, Tetration, Exponentiation, Nth Root, Logarithm, Abel Function, Logistic Function, Fixed Point, Iterated Logarithm. Betascript Publishing, Beau Bassin, Mauritius.
  16. Urroz, J. J., & Yebra, J. L. A. (2009). On the equation 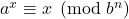a^x \equiv x \pmod {b^n} . Journal of Integer Sequences, 12(8), Article 09.2.4, 1–8.
  17. Weisstein, E. W. (2024). Graham’s Number. MathWorld – A Wolfram Web Resource. Available online at: https://mathworld.wolfram.com/GrahamsNumber.html

Manuscript history

  • Received: 15 October 2024
  • Revised: 6 September 2025
  • Accepted: 10 September 2025
  • Online First: 12 September 2025

Copyright information

Ⓒ 2025 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).

Related papers

Cite this paper

Ripà, M. (2025). Graham’s number stable digits: An exact solution. Notes on Number Theory and Discrete Mathematics, 31(3), 607-616, DOI: 10.7546/nntdm.2025.31.3.607-616.

    \[\udots\]

Comments are closed.