Affine–Hill cipher from Hadamard-type Fibonacci–Mersenne and Fibonacci-balancing p-sequences

Elahe Mehraban, T. Aaron Gulliver and Evren Hincal
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 3, Pages 588–606
DOI: 10.7546/nntdm.2025.31.3.588-606
Full paper (PDF, 229 Kb)

Details

Authors and affiliations

Elahe Mehraban
Mathematics Research Center, Near East University TRNC, Mersin 10, 99138 Nicosia, Turkey
Department of Mathematics, Near East University TRNC, Mersin 10, 99138 Nicosia, Turkey

T. Aaron Gulliver
Department of Electrical and Computer Engineering, University of Victoria, Victoria, BC V8W 2Y2, Canada

Evren Hincal
Mathematics Research Center, Near East University TRNC, Mersin 10, 99138 Nicosia, Turkey
Department of Mathematics, Near East University TRNC, Mersin 10, 99138 Nicosia, Turkey
Research Center of Applied Mathematics, Khazar University, Baku, Azerbaijan

Abstract

In this paper, we define two new sequences using the generalized Mersenne numbers, Fibonacci -numbers, and -balancing numbers. These sequences are constructed using the Hadamard-type product of their characteristic polynomials. The determinants and combinatorial and exponential representations of these new sequences are given. As an application, they are with used to generate keys for encryption for the Affine–Hill cipher using an elliptic curve and self-invertible matrix.

Keywords

• Mersenne numbers
• Fibonacci -numbers
• Elliptic curve
• Self-invertible matrix
• Affine–Hill cipher

2020 Mathematics Subject Classification

• 11K31
• 11C20
• 68P25
• 68R01
• 68P30
• 15A15

References

1. Acharya, B., Rath, G. S., Patra, S. K., & Panigrahy, S. K. (2007). Novel methods of generating self-invertible matrix for Hill cipher algorithm. International Journal of Security, 1(1), 14–21.
2. Aküzüm, Y., & Deveci, Ö. (2020). The Hadamard-type k-step Fibonacci sequences in groups. Communications in Algebra, 48(7), 2844–2856.
3. Ali-Pacha, H., Hadj-Said, N., Ali-Pacha, A., & Özer, Ö. (2020). Significant role of the specific prime number p = 257 in the improvement of cryptosystems. Notes on Number Theory and Discrete Mathematics, 26(4), 213–222.
4. Badidja, S., Mokhtar, A. A., & Özer, Ö. (2021). Representation of integers by k-generalized Fibonacci sequences and applications in cryptography. Asian-European Journal of Mathematics, 14(9), Article ID 2150157.
5. Deveci, Ö. (2019). The Jacobsthal–Padovan p-sequences and their applications. Proceedings of the Romanian Academy, Series A, 20(3), 215–224.
6. Deveci, Ö., & Shannon, A. G. (2018). The quaternion-Pell sequence. Communications in Algebra, 46(12), 5403–5409.
7. Hadj Brahim, A., Ali-Pacha, H., Naim, M., & Ali-Pacha, A. (2024). A new pseudo-random generator based on two chaotic systems. Journal of Systems Science and Information, 12(6), 775–789.
8. Hankerson, D., Vanstone, S., & Menezes, A. (2004). Guide to Elliptic Curve Cryptography. Springer-Verlag, New York.
9. Hashemi, M., & Mehraban, E. (2021). The generalized order k-Pell sequences in some special groups of nilpotency class 2. Communications in Algebra, 50(4), 1768–1784.
10. Hashemi, M., & Mehraban, E. (2022). An application of the t-extension of the p-Fibonacci Pascal matrix in coding theory. Advances in Mathematical Physics, 2022, Article ID 4619136.
11. Hill, L. S. (1929). Cryptography in an algebraic alphabet. The American Mathematical Monthly, 36(6), 306–312.
12. Hiller, J., Aküzüm, Y., & Deveci, Ö. (2018). The adjacency-Pell-Hurwitz numbers. Integers, 18, Article ID #A83.
13. Hoffstein, J. (2008). Elliptic Curves and Cryptography (Chapter 5). In: An Introduction to Mathematical Cryptography. (Silverman, J. H., & Pipher, J., Eds.), 299–371. Springer, New York.
14. Grillet, P. A. (2007). Abstract Algebra (2nd ed.). Graduate Texts in Mathematics, Vol. 242, Springer, Berlin.
15. Mehraban, E., & Hashemi, M. (2023). Fibonacci length and the generalized order k-Pell sequences of the 2-generator p-groups of nilpotency class 2. Journal of Algebra and Its Applications, 22(3), Article ID 2350061.
16. Merzoug, A., Ali-Pacha, H., Ali-Pacha, A., & Özer, Ö. (2025). Neuronal crypto system based on chaotic super-increasing sequence. Journal of Discrete Mathematical Sciences and Cryptography, 28(3), 733–751.
17. Ochalik, P., & Włoch, A. (2018). On generalized Mersenne numbers, their interpretations and matrix generators. Annales Universitatis Mariae Curie-Skłodowska. Sectio A-Mathematica, 72(1), 69–76.
18. Özkoç, A. (2015). Tridiagonal matrices via k-balancing number. British Journal of Mathematics and Computer Science, 10(4), 1–11.
19. Özkoç, A., & Tekcan, A. (2017). On k-balancing numbers. Notes on Number Theory and Discrete Mathematics, 23(3), 38–52.
20. Prasad, K., & Mahato, H. (2022). Cryptography using generalized Fibonacci matrices with Affine-Hill cipher. Journal of Discrete Mathematical Sciences and Cryptography, 25(8), 2341–2352.
21. Prasad, M. G. V., Chari, P. P. P., & Satyam, K. P. (2016). Affine Hill cipher key generation matrix of order 3 by using reflects in an arbitrary line 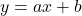. International Journal of Science Technology and Management, 5(8), 268–272.
22. Stakhov, A. P. (2006). Fibonacci matrices, a generalization of the “Cassini formula”, and new coding theory. Chaos, Solitons & Fractals, 30(1), 56–66.
23. Stinson, D. R. (2005). Cryptography: Theory and Practice (3rd ed.). Chapman and Hall/CRC, Boca Raton, FL.

Manuscript history

• Received: 9 December 2024
• Revised: 5 September 2025
• Accepted: 7 September 2025
• Online First: 10 September 2025

Copyright information

Ⓒ 2025 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).