A. D. Godase
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 3, Pages 570–582
DOI: 10.7546/nntdm.2025.31.3.570-582
Full paper (PDF, 199 Kb)
Details
Authors and affiliations
A. D. Godase ![]()
![]()
Department of Mathematics, V. P. College Vaijapur
Aurangabad, 423701, Maharashtra, India
Abstract
In this paper, we introduce a set of identities involving hyperbolic ![]() -Fibonacci quaternions and
-Fibonacci quaternions and ![]() -Lucas quaternions. Moreover, we derive summation identities for hyperbolic
-Lucas quaternions. Moreover, we derive summation identities for hyperbolic ![]() -Fibonacci and
-Fibonacci and ![]() -Lucas quaternions by utilizing established properties of
-Lucas quaternions by utilizing established properties of ![]() -Fibonacci and
-Fibonacci and ![]() -Lucas numbers. These findings add valuable insight into the relationships between these quaternion sequences and offer valuable insights into their properties.
-Lucas numbers. These findings add valuable insight into the relationships between these quaternion sequences and offer valuable insights into their properties.
Keywords
- Fibonacci quaternion
- Lucas quaternion
 -Fibonacci quaternion
-Fibonacci quaternion -Lucas quaternion
-Lucas quaternion
2020 Mathematics Subject Classification
- 11B39
- 11B37
- 11B52
References
- Bolat, C., & Köse, H. (2010). On the properties of
 -Fibonacci numbers. International Journal of Contemporary Mathematical Sciences, 5(22), 1097–1105.
-Fibonacci numbers. International Journal of Contemporary Mathematical Sciences, 5(22), 1097–1105. - Falcón, S., & Plaza, Á (2007). The
 -Fibonacci sequence and the Pascal
-Fibonacci sequence and the Pascal 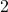 -triangle. Chaos, Solitons & Fractals, 33(1), 38–49.
-triangle. Chaos, Solitons & Fractals, 33(1), 38–49. - Godase, A. D. (2019). Properties of
 -Fibonacci and k-Lucas octonions. Indian Journal of Pure and Applied Mathematics, 50(4), 979–998.
-Fibonacci and k-Lucas octonions. Indian Journal of Pure and Applied Mathematics, 50(4), 979–998. - Godase, A. D. (2020). Hyperbolic
 -Fibonacci and
-Fibonacci and  -Lucas octonions. Notes on Number Theory and Discrete Mathematics, 26(3), 176–188.
-Lucas octonions. Notes on Number Theory and Discrete Mathematics, 26(3), 176–188. - Godase, A. D. (2021). Study of Generalized Fibonacci Sequences. Doctoral dissertation. Department of Mathematics, Dr. Babasaheb Ambedkar Marathwada University.
- Godase, A. D. (2021). Hyperbolic
 -Fibonacci and
-Fibonacci and  -Lucas quaternions. Mathematics Student, 90(1–2), 103–116.
-Lucas quaternions. Mathematics Student, 90(1–2), 103–116. - Hamilton, W. (1844). On a new species of imaginary quantities connected with a theory of quaternions. Proceedings of The Royal Irish Academy, 2, 424–434.
- Hamilton, W. (1866). Elements of Quaternions. Longmans, Green & Co., London.
- Horadam, A. (1963). Complex Fibonacci numbers and Fibonacci quaternions. The American Mathematical Monthly, 70(3), 289–291.
- Macfarlane, A. (1900). Hyperbolic quaternions. Proceedings of The Royal Society of Edinburgh, 23, 169–180.
- Polatlı, E., & Kesim, S. (2015). A note on Catalan’s identity for the
 -Fibonacci quaternions. Journal of Integer Sequences, 18(8), Article 15.8.2.
-Fibonacci quaternions. Journal of Integer Sequences, 18(8), Article 15.8.2. - Polatlı, E., Kızılates¸, C., & Kesim, S. (2016). On split
 -Fibonacci and
-Fibonacci and  -Lucas quaternions. Advances in Applied Clifford Algebras, 26, 353–362.
-Lucas quaternions. Advances in Applied Clifford Algebras, 26, 353–362. - Ramírez, J. (2015). Some combinatorial properties of the
 -Fibonacci and the
-Fibonacci and the  -Lucas quaternions. Analele ştiinţifice ale Universităţii “Ovidius” Constanţa. Seria Matematică, 23(2), 201–212.
-Lucas quaternions. Analele ştiinţifice ale Universităţii “Ovidius” Constanţa. Seria Matematică, 23(2), 201–212.
Manuscript history
- Received: 27 February 2025
- Revised: 6 August 2025
- Accepted: 17 August 2025
- Online First: 22 August 2025
Copyright information
![]() Ⓒ 2025 by the Author.
Ⓒ 2025 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
- Godase, A. D. (2020). Hyperbolic
 -Fibonacci and
-Fibonacci and  -Lucas octonions. Notes on Number Theory and Discrete Mathematics, 26(3), 176–188.
-Lucas octonions. Notes on Number Theory and Discrete Mathematics, 26(3), 176–188.
Cite this paper
Godase, A. D. (2025). New summation identities of hyperbolic k-Fibonacci and k-Lucas quaternions. Notes on Number Theory and Discrete Mathematics, 31(3), 570-582, DOI: 10.7546/nntdm.2025.31.3.570-582.


