Volume 10, 2004, Number 3

Let (P, ∧) be a meet-semilattice and let S = {x₁, x₂, …, x_n} be a subset of P. We say that S is an A-set if A = {x_i ∧ x_j | x_i ≠ x_j} is a chain. For example, chains and a-sets (with A = {a}) are known trivial A-sets. The meet matrix (S)_f on S with respect to a function f : P → C is defined as ((S)_f)_ij = f(x_i ∧ x_j).

We present a recursive structure theorem for meet matrices on A-sets and thus obtain a recursive formula for det(S)_f and for (S)_f⁻¹ on A-sets. The recursive formulae also yield explicit formulae, e.g. the known determinant and inverse formulae on chains and a-sets. We also present the dual forms of our results, i.e. the determinant formulae and the inverse formulae for join matrices on join-semilattices. Finally, we suggest how our results can be generalized to more complicated cases.

As special cases these results hold also for GCD and LCM matrices and for their unitary analogies GCUD and LCUM matrices.

For the integer number n ≥ 1 written in the basis b ≥ 2, we denote by s_b(n), p_b(n) and d_b(n) the sum, the product and the number of its digits, respectively. There are a series of more recent or older papers concerning the relationship between these numbers. For instance, one proves in {2} that, if b ≥ 3, then for infinitely many numbers m there exists n with d_b(n) = m and s_b(n) = m, and this property fails also for infinitely many values of m.

The extended Euler-prime-generating equation is shown to be compatible with the composite grid of the modular ring Z₆. Invalid values of the variable x (those x values which yield composites) follow regular sequences within the grid and have associated couples within the modular ring which are linked to the prime values.

With the exception of 2 and 3, primes are only found in two classes of the modular ring Z₆. The rows of the tabular display of this ring which con­tain composites in these two classes are given by R = R₀+ pt, t = 0, 1, 2, 3, …, in which R₀ is a function of p that is class specific. The number of composites, n_c, in the two classes can be calculated from:

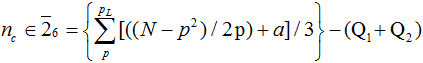
(a = 1 or 2 depending on the class of p),

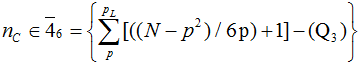
where p_L is the prime less than and closest to √N. The Q_i terms are quantities which arise from the characteristics of the factors of the composites. Subtraction of n_c from the total integers in each class yields the number of primes for that class, and hence the total number of primes in the interval.