Volume 10 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Some properties of Fermatian numbers
Original research paper. Pages 25–33
A. G. Shannon
Full paper (152 Kb) | Abstract
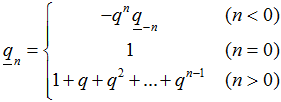
so that 1n = n, and 1n! = n!, where qn! = qnqn−1…q1.
Some congruence properties and relationships with Bernoulli and Fibonacci numbers are explored. Some aspects of the notation and meaning of the Fermatian numbers are also outlined.
On five Smarandache’s problems
Original research paper. Pages 34–53
Mladen V. Vassilev-Missana and Krassimir T. Atanassov
Full paper (5956 Kb)
Some representations concerning the product of divisors of n
Original research paper. Pages 54–56
Mladen Vassilev-Missana
Full paper (896 Kb) | Abstract
(1) ![]()
and of course, we have
(2) ![]()
But (1) is not a good formula for ![]() , because it depends on function
, because it depends on function ![]() and to express
and to express ![]() we need the prime number factorization of
we need the prime number factorization of ![]() .
.
Below, we give other representations of ![]() and
and ![]() , which do not use the prime number factorization of
, which do not use the prime number factorization of ![]() .
.


