Anthony G. Shannon, Peter J.-S. Shiue, Tian-Xiao He, and Christopher Saito
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 3, Pages 504–534
DOI: 10.7546/nntdm.2025.31.3.504-534
Full paper (PDF, 325 Kb)
Details
Authors and affiliations
Anthony G. Shannon ![]()
![]()
Warrane College, The University of New South Wales
Kensington, NSW 2033, Australia
Peter J.-S. Shiue ![]()
![]()
Department of Mathematical Sciences, University of Nevada, Las Vegas
Las Vegas, Nevada, 89154-4020, USA
Tian-Xiao He ![]()
![]()
Department of Mathematics, Illinois Wesleyan University
Bloomington, Illinois 61702, USA
Christopher Saito ![]()
![]()
Department of Mathematical Sciences, University of Nevada, Las Vegas
Las Vegas, Nevada, 89154-4020, USA
Abstract
Euler’s totient function, ![]() , is the arithmetic function defined as the number of positive integers less than or equal to
, is the arithmetic function defined as the number of positive integers less than or equal to ![]() that are relatively prime to
that are relatively prime to ![]() . In his 1922 paper [3], Professor R. D. Carmichael conjectured that for each positive integer
. In his 1922 paper [3], Professor R. D. Carmichael conjectured that for each positive integer ![]() , there exists at least one positive integer
, there exists at least one positive integer ![]() such that
such that ![]()
In this paper, we consider some relevant literature and explore Carmichael’s totient conjecture for particular values of ![]() Our main consideration will be the set
Our main consideration will be the set ![]() . In identifying
. In identifying ![]() for
for ![]() and
and ![]() , where
, where ![]() and
and ![]() are distinct prime numbers, we find that Carmichael’s conjecture holds for those select cases, provide an algorithm, and some related results. The conjecture remains an open problem in number theory [9].
are distinct prime numbers, we find that Carmichael’s conjecture holds for those select cases, provide an algorithm, and some related results. The conjecture remains an open problem in number theory [9].
Keywords
- Carmichael Conjecture
- Euler totient function
- Fermat chain
- Fermat primes
- Fibonacci numbers
- Germain primes
- Integer components
- Primitive prime divisors
2020 Mathematics Subject Classification
- 11A07
- 11Y11
References
- Carmichael, R. D. (1908). A table of the values of m corresponding to given values of ϕ(m). American Journal of Mathematics, 30(4), 394–400.
- Carmichael, R. D. (1919). Fermat numbers
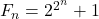 . The American Mathematical Monthly, 26(4), 137–146.
. The American Mathematical Monthly, 26(4), 137–146. - Carmichael, R. D. (1922). Note on Euler’s φ-function. Bulletin of the American Mathematical Society, 28(3), 109–110.
- Dickson, L. E. (1919). History of the Theory of Numbers, Vol. 1. Chelsea, New York.
- Donnelly, H. (1973). On a problem concerning Euler’s phi-function. The American Mathematical Monthly, 80(9), 1029–1031.
- Ford, K. (1998). The distribution of totients. The Ramanujan Journal, 2, 67–151.
- Grosswald, P. (1973). Contribution to the theory of Euler’s function φ(x). Bulletin of the American Mathematical Society, 79(2), 337–341.
- Gupta, H. (1981). Euler’s totient function and its inverse. Indian Journal of Pure and Applied Mathematics, 12(1), 22–30.
- Guy, R. (2004). Unsolved Problems in Number Theory, Vol. 3. Springer, New York.
- Holt, J. J. (2003). The minimal number of solutions to
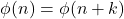 . Mathematics of Computation, 72(244), 2059–2061.
. Mathematics of Computation, 72(244), 2059–2061. - Iverson, K. E. (1980). Notation as a tool of thought. Communications of the ACM, 23(8), 444–465.
- Klee, V. L., Jr. (1947). On a conjecture of Carmichael. Bulletin of the American Mathematical Society, 53(12), 1183–1186.
- Leveque, W. J. (1974). Reviews in Number Theory 1940–1972: As printed in Mathematical Reviews 1940-1972. American Mathematical Society, Providence.
- Mahatmya, D., Morrison, J., Jones, R. M., Garner, P. W., Davis, S. N., Manske, J., Berner, N., Johnson, A., & Ditty, J. (2017). Pathways to undergraduate research experiences: A multi-institutional study. Innovative Higher Education, 42(5–6), 591–504.
- Masai, P., & Valette, A. (1982). A lower bound for a counterexample to Carmichael’s conjecture. Bollettino della Unione Matemàtica Italiana. Serie VI. A, 1(2), 313–316.
- Mendelsohn, N. S. (1976). The equation
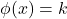 . Mathematics Magazine, 49(1), 37–39.
. Mathematics Magazine, 49(1), 37–39. - Merow, S. D. (2019). Has Carmichael’s conjecture been proven? No, no, it has not. Notices of the American Mathematical Society, 66(5), 759–761.
- Olunloyo, V. O. S. (1975). On the numerical solution of a Diophantine equation connected with near-primality. Abacus, 10, 123–144.
- Pichler, A. (1900–1901). Über die Auflösung der Gleichung:
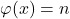 , wenn
, wenn 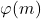 die Anzahl derjenigen Zahlen bezeichnet, welche relativ prim zu
die Anzahl derjenigen Zahlen bezeichnet, welche relativ prim zu 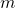 und kleiner als
und kleiner als 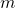 sind. Jahresbericht des K. K. Maximilian-Gymnasiums in Wien, 3–17.
sind. Jahresbericht des K. K. Maximilian-Gymnasiums in Wien, 3–17. - Polya, G. (1957). How to Solve It: A New Aspect of Mathematical Method (2nd edition). Princeton University Press, Princeton.
- Pomerance, C. (1974). On Carmichael’s conjecture. Proceedings of the American Mathematical Society, 43(2), 297–298.
- Ramadan-Jradi, W. (1999). Carmichael’s conjecture and a minimal unique solution. Notes on Number Theory and Discrete Mathematics, 5(2), 55–70.
- Rosen, K. H. (2011). Elementary Number Theory and Its Applications (6th edition). Pearson Addison-Wesley.
- Schinzel, A. (1961). Remarks on the paper “Sur certaines hypothèses concernant les nombres premiers”. Acta Arithmetica, 7(1), 1–8.
- Schlafly, A., & Wagon, S. (1994). Carmichael’s conjecture on the Euler function is valid below
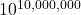 . Mathematics of Computation, 63(207), 415–419.
. Mathematics of Computation, 63(207), 415–419. - Sivaramakrishnan, R. (1986). The many facets of Euler’s totient I: A general perspective. Nieuw Archief voor Wiskunde, 4, 175–190.
- Sloane, N. J. A. (2023). A005384 Sophie Germain primes: Sophie Germain primes
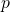 :
: 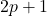 is also prime. The On-Line Encyclopedia of Integer Sequences. Available online at: https://oeis.org/A005384.
is also prime. The On-Line Encyclopedia of Integer Sequences. Available online at: https://oeis.org/A005384. - Spyropoulos, K. (1989). Euler’s equation
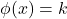 with no solution. Journal of Number Theory, 32(2), 254–256.
with no solution. Journal of Number Theory, 32(2), 254–256. - Stepanova, L. L., & Flikop, E. L. (1972). On the question of the number of solutions of the equation
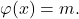 Studies in Number Theory Izdat Saratov University, 4, 89–93.
Studies in Number Theory Izdat Saratov University, 4, 89–93. - Vassilev-Missana, M. (1996). Note on the equation φ(x) = 2l.q. Notes on Number Theory and Discrete Mathematics, 2(3), 45–46.
- Vassilev-Missana, M. (1996). The numbers which cannot be values of Euler’s function φ. Notes on Number Theory and Discrete Mathematics, 2(4), 41–48.
- Wegner, K. W., & Savitsky, S. R. (1970). Solutions of
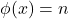 , where
, where 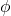 is Euler’s
is Euler’s 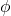 -function. The American Mathematical Monthly, 77(3), 287.
-function. The American Mathematical Monthly, 77(3), 287.
Manuscript history
- Received: 19 May 2025
- Revised: 28 July 2025
- Accepted: 4 August 2025
- Online First: 15 August 2025
Copyright information
![]() Ⓒ 2025 by the Authors.
Ⓒ 2025 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
- Ramadan-Jradi, W. (1999). Carmichael’s conjecture and a minimal unique solution. Notes on Number Theory and Discrete Mathematics, 5(2), 55–70.
- Vassilev-Missana, M. (1996). The numbers which cannot be values of Euler’s function φ. Notes on Number Theory and Discrete Mathematics, 2(4), 41–48.
- Vassilev-Missana, M. (1996). Note on the equation φ(x) = 2l.q. Notes on Number Theory and Discrete Mathematics, 2(3), 45–46.
Cite this paper
Shannon, A. G., Shiue, P. J.-S., He, T.-X., & Saito, C. (2025). On the special cases of Carmichael’s totient conjecture. Notes on Number Theory and Discrete Mathematics, 31(3), 504-534, DOI: 10.7546/nntdm.2025.31.3.504-534.


