Volume 16 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
On the Diophantine equation 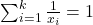 in distinct integers of the form
in distinct integers of the form 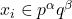
Original research paper. Pages 1–5
Nechemia Burshtein
Full paper (PDF, 156 Kb) | Abstract
A complete demonstration of solutions of the above Diophantine equation is given when
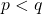
are primes and
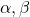
are positive integers. Among the several examples exhibited, Example 3 provides a new solution containing eighty-five even numbers
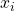
all of which are of the required form. Certain questions and modifications of the equation are also discussed.
Integer structure analysis of odd powered triples: The significance of triangular versus pentagonal numbers
Original research paper. Pages 6–13
J. V. Leyendekkers, A. Shannon
Full paper (PDF, 168 Kb) | Abstract
Structural constraints prevent the difference of two odd cubes ever equaling an even cube. This is illustrated from the row structure of the modular ring Z4. The critical structure factor is that the rows of integers, N2, with 3 | N2, follow the triangular numbers, whereas 3 ∤ N2 rows follow the pentagonal numbers. This structural characteristic is the reason for the importance of primitive Pythagorean triples (in which either the smallest odd component or the even component always has a factor 3).
Fermatian analogues of Gould’s generalized Bernoulli polynomials
Original research paper. Pages 14–17
A. G. Shannon
Full paper (PDF, 117 Kb) | Abstract
Some results of Gould for the ordinary Bernoulli and Euler polynomials are extended to analogous results built upon the Fermatian exponentials.
Combined 2-Fibonacci sequences. Part 2
Original research paper. Pages 18–24
Krassimir T. Atanassov
Full paper (PDF, 126 Kb) | Abstract
Two new sequences from Fibonacci type are introduced and the explicit formulae for their n-th members are given.
Sharp concentration of the rainbow connection of random graphs
Original research paper. Pages 25–28
Yilun Shang
Full paper (PDF, 145 Kb) | Abstract
An edge-colored graph G is rainbow edge-connected if any two vertices are connected by a path whose edges have distinct colors. The rainbow connection of a connected graph G, denoted by rc(G), is the smallest number of colors that are needed in order to make G rainbow connected. Similarly, a vertex-colored graph G is rainbow vertex-connected if any two vertices are connected by a path whose internal vertices have distinct colors. The rainbow vertex-connection of a connected graph G, denoted by rvc(G), is the smallest number of colors that are needed in order to make G rainbow vertex-connected. We prove that both rc(G) and rvc(G) have sharp concentration in classical random graph model G(n, p).
Some results on multiplicative functions
Original research paper. Pages 29–40
Mladen Vassilev-Missana
Full paper (PDF, 237 Kb) | Abstract
In the present paper some new results, concerning multiplicative functions with strictly positive values, are obtained. In particular, it is shown that if an ordered pair of such functions (f, g) has a certain property (called in the paper S), then for every fixed positive integer n; the minimal and the maximal elements of the set {f(d)g(n/d) : d runs over all divisors of n} are obtained at least for some unitary divisors of n. For these divisors if the maximum of f(d)g(n/d) is reached for d*; then the minimum is reached for n/d* and vice versa (the main results here are Theorems 1-4). The same investigation is made, but when d runs over the set of all divisors of n different than 1 and n (the main result here is Theorem 5). Also corollaries of the mentioned results are obtained and some particular cases are considered.
Volume 16 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
![]() in distinct integers of the form
in distinct integers of the form ![]()


