On the Diophantine equation \sum_{i=1}^k \frac{1}{x_i} = 1 in distinct integers of the form x_i \in p^{\alpha}q^{\beta}

Nechemia Burshtein
Notes on Number Theory and Discrete Mathematics
ISSN 1310–5132
Volume 16, 2010, Number 4, Pages 1–5
Full paper (PDF, 156 Kb)

Details

Authors and affiliations

Nechemia Burshtein
117 Arlozorov Street, Tel Aviv 62098, Israel

Abstract

A complete demonstration of solutions of the above Diophantine equation is given when p < q are primes and  \alpha, \beta are positive integers. Among the several examples exhibited, Example 3 provides a new solution containing eighty-five even numbers x_i all of which are of the required form. Certain questions and modifications of the equation are also discussed.

Keywords

  • Diophantine equations
  • Egyptian fractions

AMS Classification

  • 11D68

References

  1. N. Burshtein. On distinct unit fractions whose sum equals 1, Discrete Math. 300 (2005) 213–217.
  2. N. Burshtein. Improving solutions of 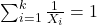\sum_{i=1}^k \frac{1}{X_i} = 1 with restrictions as required by Barbeau respectively by Johnson, Discrete Math. 306 (2006) 1438–1439.
  3. N. Burshtein. The equation 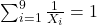\sum_{i=1}^9 \frac{1}{X_i} = 1 in distinct odd integers has only the five known solutions, Journal of Number Theory 127 (2007), 136–144.
  4. N. Burshtein. All the solutions of the equation 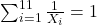\sum_{i=1}^{11} \frac{1}{X_i} = 1 in distinct integers of the form 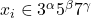x_i \in 3^{\alpha}5^{\beta} 7^{\gamma}, Discrete Math. 308 (2008), 4286–4292.
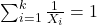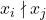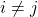  5. N. Burshtein. An improved solution of \sum_{i=1}^k \frac{1}{X_i} = 1 in distinct integers when x_i \nmid x_j for i \ne j. Notes on Number Theory and Discrete Mathematics, 16, (2010), 2, 1–4.
  6. C. Rivera, J. Ayala. The prime puzzles & problems connection – problem 35,
    http://www.primepuzzles.net/.

Related papers

Cite this paper

Burshtein, N. (2010). On the Diophantine equation \sum_{i=1}^k \frac{1}{X_i} = 1 in distinct integers of the form xi pαqβ. Notes on Number Theory and Discrete Mathematics, 16(4), 1-5.

Comments are closed.