Fermatian row and column sums as a family of generalized integers

Anthony G. Shannon, Mine Uysal and Engin Özkan
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 3, Pages 433–442
DOI: 10.7546/nntdm.2025.31.3.433-442
Full paper (PDF, 1036 Kb)

Details

Authors and affiliations

Anthony G. Shannon
Warrane College, University of New South Wales
Kensington, NSW 2033, Australia

Mine Uysal
Department of Mathematics, Faculty of Arts and Sciences, Erzincan Binali Yildirim University
Erzincan, Türkiye

Engin Özkan
Department of Mathematics, Faculty of Science, Marmara University
Istanbul, Türkiye

Abstract

In this paper, we introduce some feature of the Fermatian numbers. The finite sum formulas of these numbers is calculate. The exponential generating function of Fermatian numbers is found and some of its identities is calculated. Another number sequence is obtained from the partial row sums of these numbers and these numbers were examined. At the same time, another polynomial has been defined as a generalization of these numbers, depending on powers of z.

Keywords

  • Fermatian numbers
  • Fibonacci numbers
  • Generalized integers
  • Jacobsthal sequences
  • Recurrence relations

2020 Mathematics Subject Classification

  • 11B39
  • 01A30
  • 97A40

References

  1. Barry, P. (2006). On integer-sequence-based constructions of generalized Pascal triangles. Journal of Integer Sequences, 9, Article ID 06.2.4
  2. Carlitz, L. (1940). A set of polynomials. Duke Mathematical Journal, 6(2), 486–504.
  3. Carlitz, L. (1948). q-Bernoulli numbers and polynomials. Duke Mathematical Journal, 15(4), 987–1000.
  4. Carlitz, L., & Moser, L. (1966). On some special factorizations of 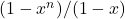(1-x^n) / (1 -x). Canadian Mathematical Bulletin, 9(4), 421–426.
  5. da Fonseca, C., & Shannon, A. G. (2024). A formal operator involving Fermatian numbers. Notes on Number Theory and Discrete Mathematics, 30(3), 491–498.
  6. Fontené, G. (1915). Généralisation d’une formule connue. Nouvelles Annales Mathématiques: Journal des candidats aux écoles polytechnique et normale, Serie 4, 15, 112.
  7. Gould, H. W. (1969). The bracket function and Fontené–Ward generalized binomial coefficients with application to Fibonomial coefficients. The Fibonacci Quarterly, 7(1), 23–40, 55.
  8. Hoggatt, V. E. Jr., & Bicknell, M. (1969). Diagonal sums of generalized Pascal triangles. The Fibonacci Quarterly, 7(4), 341–358.
  9. Horadam, A. F., & Treweek, A. P. (1986). Simson’s formula and an equation of degree 24. The Fibonacci Quarterly, 24(4), 344–346.
  10. Horadam, E. M. (1971). An extension of Daykin’s generalized Möbius function to unitary divisors. Journal für die reine und angewandte Mathematik, 246, 117–125.
  11. Macmahon, P. A. (1916). Combinatory Analysis. Cambridge University Press, Cambridge.
  12. Sándor, J., & Atanassov, K. T. (2021). Arithmetic Functions. Nova Science Publishers, New York.
  13. Shanks, D. (1993). Solved and Unsolved Problems in Number Theory (4th ed). Chelsea, New York, pp. 115–117.
  14. Shannon, A. G. (2010). Fermatian analogues of Gould’s generalized Bernoulli polynomials. Notes on Number Theory and Discrete Mathematics, 16(4), 14–17.
  15. Shannon, A. G. (2014). Fermatian Hurwitz series within the Fontené–Jackson calculus. Advanced Studies in Contemporary Mathematics, 24(1), 129–136.
  16. Shannon, A. G. (2019). Applications of Mollie Horadam’s generalized integers to Fermatian and Fibonacci numbers. Notes on Number Theory and Discrete Mathematics, 25(2), 113–126.
  17. Sloane, N. J. A., & Plouffe, S. (1973). The Encyclopedia of Integer Sequences. Academic Press, San Diego, CA. Available online at: http://oeis.org.
  18. Ward, M. (1936). A calculus of sequences. American Journal of Mathematics, 58(2), 255–266.

Manuscript history

  • Received: 13 July 2025
  • Revised: 25 July 2025
  • Accepted: 26 July 2025
  • Online First: 28 July 2025

Copyright information

Ⓒ 2025 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).

Related papers

  1. da Fonseca, C., & Shannon, A. G. (2024). A formal operator involving Fermatian numbers. Notes on Number Theory and Discrete Mathematics, 30(3), 491–498.
  2. Shannon, A. G. (2019). Applications of Mollie Horadam’s generalized integers to Fermatian and Fibonacci numbers. Notes on Number Theory and Discrete Mathematics, 25(2), 113–126.
  3. Shannon, A. G. (2010). Fermatian analogues of Gould’s generalized Bernoulli polynomials. Notes on Number Theory and Discrete Mathematics, 16(4), 14–17.

Cite this paper

Shannon, A. G., Uysal, M., & Özkan, E. (2025). Fermatian row and column sums as a family of generalized integers. Notes on Number Theory and Discrete Mathematics, 31(3), 433-442, DOI: 10.7546/nntdm.2025.31.3.433-442.

Comments are closed.