Almost repdigits in balancing and Lucas-balancing sequences

Manasi K. Sahukar and Hussain Basha
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 2, Pages 390–403
DOI: 10.7546/nntdm.2025.31.2.390-403
Full paper (PDF, 251 Kb)

Details

Authors and affiliations

Manasi K. Sahukar
Department of Mathematics, S. K. C. G. Autonomous College
Paralakhemundi, 761200 Odisha, India

Hussain Basha
Department of Mathematics, Government First Grade College
Zalaki-586204, Karnataka, India

Abstract

In this paper, we define the notion of almost repdigit as a positive integer whose digits are all equal except for at most one digit, and we search all terms of the balancing and Lucas-balancing sequences which are almost repdigits. In particular, the only almost repdigits in balancing sequence are 0, 1, 6, and the only almost repdigits in Lucas-balancing sequence are 1, 3, 17, 99, 577, 3363.

Keywords

  • Diophantine equations
  • Linear form of logarithms
  • Almost repdigits
  • Balancing numbers
  • Lucas-balancing numbers

2020 Mathematics Subject Classification

  • 11A25
  • 11B39

References

  1. Altassan, A., & Alan, M. (2023). Almost repdigit k-Fibonacci numbers with an application of k-generalized Fibonacci sequences. Mathematics, 11(2), Article ID 455.
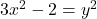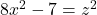  2. Baker, A., & Davenport, H. (1969). The equations 3x^2-2=y^2 and 8x^2-7=z^2. The Quarterly Journal of Mathematics, 20, 129–137.
  3. Behera, A., & Panda, G. K. (1999). On the square roots of triangular numbers. The Fibonacci Quarterly, 37(2), 98–105.
  4. Bravo, J. J., Gómez, C.A.G., & Luca, F. (2016). Powers of two as sums of two k-Fibonacci numbers. Miskolc Mathematical Notes, 17(1), 85–100.
  5. Bugeaud, Y., Mignotte, M., & Siksek, S. (2006). Classical and modular approaches to exponential Diophantine equations I. Fibonacci and Lucas perfect powers. Annals of Mathematics, 163(3), 969–1018.
  6. Dujella, A., & Petho, A. (1998). A generalization of a theorem of Baker and Davenport. Quarterly Journal of Mathematics, Oxford Series, 49, 291–306.
  7. Faye, B., & Luca, F. (2015). Pell and Pell–Lucas numbers with only one distinct digit. Annales Mathematicae et Informaticae, 45, 55–60.
  8. Gica, A., & Panaitopol, L. (2003). On Obláth’s problem. Journal of Integer Sequences, 6(3), Article ID 03.3.5.
  9. Irmak, N., & Togbé, A. (2018). On repdigits as product of consecutive Lucas numbers. Notes on Number Theory and Discrete Mathematics, 24(3), 95–102.
  10. Kihel, O., & Luca, F. (2005). Perfect powers with all equal digits but one. Journal of Integer Sequences, 8(5), Article ID 05.5.7.
  11. Luca, F. (2000). Fibonacci and Lucas numbers with only one distinct digit. Portugaliae Mathematica, 57(2), 243–254.
  12. Matveev, E. M. (2000). An explicit lower bound for a homogeneous rational linear forms in logarithms of algebraic numbers, II. Izvestiya Rossiĭskoĭ Akademii Nauk. Seriya Matematicheskaya, 64, 125–180. [English translation: Izvestiya: Mathematics, 64, 1217–1269.]
  13. Panda, G. K. (2009). Some fascinating properties of balancing numbers. Proceedings of the Eleventh International Conference on Fibonacci Numbers and Their Applications, Braunschweig, Germany, July 5–9, 2004. Congressus Numerantium, 194, 185–189.
  14. Rayaguru, S. G., & Bravo, J. J. (2023). Balancing and Lucas-balancing numbers which are concatenation of three repdigits. Boletín de la Sociedad Matemática Mexicana, 29, Article ID 57.
  15. Rayaguru, S. G., & Panda, G. K. (2018). Repdigits as product of consecutive balancing and Lucas-balancing numbers. The Fibonacci Quarterly, 56(4), 319–324.
  16. Rayaguru, S. G., & Panda, G. K. (2020). Balancing numbers which are concatenation of two repdigits. Boletín de la Sociedad Matemática Mexicana, 26(3), 911–919.
  17. Rayaguru, S. G., & Panda, G. K. (2021). Balancing and Lucas-balancing numbers
    expressible as sums of two repdigits. Integers, 21, Article ID #A7.
  18. Sahukar, M. K., & Panda, G. K. (2019). Repdigits in Euler functions of Pell numbers. The Fibonacci Quarterly, 57(2), 134-–138.
  19. Sahukar, M. K., & Panda, G. K. (2020). Repdigits in Euler functions of associated Pell numbers. Proceedings – Mathematical Sciences, 130(1), Article ID 25.
  20. de Weger, B. M. M. (1989). Algorithms for Diophantine Equations. CWI Tracts, Vol. 65, Centrum voor Wiskunde en Informatica, Amsterdam.

Manuscript history

  • Received: 29 November 2024
  • Revised: 9 June 2025
  • Accepted: 12 June 2025
  • Online First: 14 June 2025

Copyright information

Ⓒ 2025 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).

Related papers

Cite this paper

Sahukar, M. K., & Basha, H. (2025). Almost repdigits in balancing and Lucas-balancing sequences. Notes on Number Theory and Discrete Mathematics, 31(2), 390-403, DOI: 10.7546/nntdm.2025.31.2.390-403.

Comments are closed.