Euclidean tours in fairy chess

Gabriele Di Pietro and Marco Ripà
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 1, Pages 54–68
DOI: 10.7546/nntdm.2025.31.1.54-68
Full paper (PDF, 254 Kb)

Details

Authors and affiliations

Gabriele Di Pietro
Roseto degli Abruzzi (TE), Italy

Marco Ripà
World Intelligence Network
Rome, Italy

Abstract

The present paper aims to generalize the Knight’s tour problem for k-dimensional grids of the form \{0,1\}^k by considering other fairy chess leapers. Accordingly, we constructively show the existence of closed tours in 2 \times 2 \times \cdots \times 2 (k times) chessboards concerning the Wazir, the Threeleaper, and the Zebra, for all k \geq 15. This extends the recent discovery of Euclidean Knight’s tours on these grids to the above-mentioned leapers, opening a new research direction on fairy chess leapers performing fixed-length jumps on regular grids.

Keywords

  • Fairy chess
  • Euclidean tour
  • Knight’s tour
  • Zebra’s tour
  • Hamiltonian path

2020 Mathematics Subject Classification

  • 05C12
  • 05C38
  • 05C57

References

  1. Brown, A. J. (2017). Knight’s Tours and Zeta Functions (MS thesis). San José State University, p. 3.
  2. Cancela, H., & Mordecki, E. (2015). On the number of open knight’s tours. Preprint. arXiv.org, Available online at: https://arxiv.org/abs/1507.03642.
  3. Di Pietro, G., & Ripà, M. (2024). Threeleaper’s Euclidean tour on the 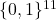\{0, 1\}^{11} grid – data file supporting Euclidean tours in fairy chess. Zenodo.org. Available online at: https://zenodo.org/records/11199717.
  4. Di Pietro, G., & Ripà, M. (2024). Zebra’s Euclidean tour on the 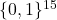\{0, 1\}^{15} grid – data file supporting Euclidean tours in fairy chess. Zenodo.org. Available online at: https://zenodo.org/records/11490687.
  5. Dickins, A. S. M. (1969). A Guide to Fairy Chess. The Q Press, Richmond, Surrey.
  6. Dvořák, T., & Gregor, P. (2007). Hamiltonian paths with prescribed edges in hypercubes. Discrete Mathematics, 307(16), 1982–1998.
  7. Euler, L. (1759). Solution dune question curieuse que ne paroit soumise à aucune analyse. Mémoires de l’académie des sciences de Berlin, 15, 310–337.
  8. FIDE (2022). FIDE Handbook E/01 – Laws of Chess. FIDE.com, Available online at: https://www.fide.com/FIDE/handbook/LawsOfChess.pdf.
  9. Harary, F., Hayes, J. P., & Wu, H.-J. (1988). A survey of the theory of hypercube graphs. Computers & Mathematics with Applications, 15(4), 277–289.
  10. Hooper, D., & Whyld, K. (1996). Knight’s Tour. Oxford University Press, Oxford, p. 204.
  11. Ripà, M. (2023). Metric spaces in chess and international chess pieces graph diameters. Preprint. arXiv.org. Available at: https://arxiv.org/abs/2311.00016.
  12. Ripà, M. (2024). Proving the existence of Euclidean knight’s tours on n × n × ··· × n chessboards for n < 4. Notes on Number Theory and Discrete Mathematics, 30(1), 20–33.
  13. Satyadev, C. (1991). Kavyalankara of Rudrata, with Hindi translation. Delhitraversal: Parimal Sanskrit Series No. 30. Parimal Publications, Delhi.

Manuscript history

  • Received: 13 June 2024
  • Revised: 31 March 2025
  • Accepted: 1 April 2025
  • Online First: 2 April 2025

Copyright information

Ⓒ 2025 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).

Related papers

Cite this paper

Di Pietro, G., & Ripà, M. (2025). Euclidean tours in fairy chess. Notes on Number Theory and Discrete Mathematics, 31(1), 54-68, DOI: 10.7546/nntdm.2025.31.1.54-68.

Comments are closed.