Djamel Bellaouar, Özen Özer and Noureddine Azzouza
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 1, Pages 191–200
DOI: 10.7546/nntdm.2025.31.1.191-200
Full paper (PDF, 290 Kb)
Details
Authors and affiliations
Djamel Bellaouar ![]()
![]()
Department of Mathematics, University 8 Mai 1945 Guelma
B.P. 401 Guelma 24000, Algeria
Özen Özer ![]()
![]()
Department of Mathematics, University of Kırklareli
39000, Kirklareli, Türkiye
Noureddine Azzouza ![]()
![]()
Department of Mathematics, University 8 Mai 1945 Guelma
B.P. 401 Guelma 24000, Algeria
Abstract
Consider the Padovan sequence ![]() given by
given by ![]() with
with ![]() Its companion sequence, the Perrin sequence
Its companion sequence, the Perrin sequence ![]() follows the same recursive formula as the Padovan numbers, but with different initial values:
follows the same recursive formula as the Padovan numbers, but with different initial values: ![]() and
and ![]() In this paper, we leverage Baker’s theory concerning nonzero linear forms in logarithms of algebraic numbers along with a reduction procedure that employs the theory of continued fractions. This enables us to explicitly identify all Padovan and Perrin numbers that conform to the representation
In this paper, we leverage Baker’s theory concerning nonzero linear forms in logarithms of algebraic numbers along with a reduction procedure that employs the theory of continued fractions. This enables us to explicitly identify all Padovan and Perrin numbers that conform to the representation ![]() where
where ![]() and
and ![]() are positive integers with
are positive integers with ![]()
Keywords
- Exponential Diophantine equations
- Padovan numbers
- Perrin numbers
- Linear forms in logarithms
2020 Mathematics Subject Classification
- 11B37
- 11D61
- 11J86
References
- Adedji, K. N., Filipin, A., & Togbé, A. (2021). Padovan and Perrin numbers which are products of two repdigits in base b. Results in Mathematics, 76(4), Article ID 193.
- Batte, H., Chalebgwa, T. P., & Ddamulira, M. (2022). Perrin numbers that are
concatenations of two repdigits. Arabian Journal of Mathematics, 11(3), 469–478. - Bugeaud, Y., Mignotte, M., & Siksek, S. (2006). Classical and modular approaches to exponential Diophantine equations I. Fibonacci and Lucas perfect powers. Annals of Mathematics, 163(3), 969–1018.
- Dujella, A., & Pethő, A. (1998). A generalization of a theorem of Baker and Davenport. The Quarterly Journal of Mathematics, 49(3), 291–306.
- Irmak, N., & Alp, M. (2017). k-generalized Fibonacci numbers close to the form
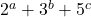 . Acta Mathematica Universitatis Comenianae, 86(2), 279–286.
. Acta Mathematica Universitatis Comenianae, 86(2), 279–286. - Luca, F., & Szalay, L. (2007). Fibonacci numbers of the form
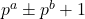 . The Fibonacci Quarterly, 45(2), 98–103.
. The Fibonacci Quarterly, 45(2), 98–103. - Marques, M. (2014). Generalized Fibonacci numbers of the form
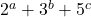 . Bulletin of the Brazilian Mathematical Society, New Series, 45(3), 543–557.
. Bulletin of the Brazilian Mathematical Society, New Series, 45(3), 543–557. - Marques, D., & Togbé, A. (2013). Fibonacci and Lucas numbers of the form
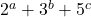 . Proceedings of the Japan Academy, Series A: Mathematical Sciences, 89(3), 47–50.
. Proceedings of the Japan Academy, Series A: Mathematical Sciences, 89(3), 47–50. - Matveev, E. M. (2000). An explicit lower bound for a homogeneous rational linear form in the logarithms of algebraic numbers. II. Izvestiya: Mathematics, 64(6), 1217–1269.
- Qu, Y., Zeng, J., & Cao, Y. (2018). Fibonacci and Lucas numbers of the form
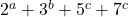 . Symmetry, 10(10), Article ID 509.
. Symmetry, 10(10), Article ID 509. - Sokhuma, K. (2013). Matrices formula for Padovan and Perrin sequences. Applied Mathematical Sciences, 7(142) 7093–7096.
Manuscript history
- Received: 5 May 2024
- Revised: 20 October 2024
- Accepted: 28 April 2025
- Online First: 30 April 2025
Copyright information
![]() Ⓒ 2025 by the Authors.
Ⓒ 2025 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Bellaouar, D., Özer, Ö, & Azzouza, N. (2025). Padovan and Perrin numbers of the form ![]() . Notes on Number Theory and Discrete Mathematics, 31(1), 191-200, DOI: 10.7546/nntdm.2025.31.1.191-200.
. Notes on Number Theory and Discrete Mathematics, 31(1), 191-200, DOI: 10.7546/nntdm.2025.31.1.191-200.


