On (k,p)-Fibonacci numbers and matrices

Sinan Karakaya, Halim Özdemir and Tuğba Demirkol
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 30, 2024, Number 4, Pages 735–744
DOI: 10.7546/nntdm.2024.30.4.735-744
Full paper (PDF, 253 Kb)

Details

Authors and affiliations

Sinan Karakaya
Department of Mathematics, University of Sakarya
54187, Serdivan, Sakarya, Turkey

Halim Özdemir
Department of Mathematics, University of Sakarya
54187, Serdivan, Sakarya, Turkey

Tuğba Demirkol
Department of Mathematics, University of Sakarya
54187, Serdivan, Sakarya, Turkey

Abstract

In this paper, some relations between the powers of any matrices satisfying the equation and -Fibonacci numbers are established with . First, a result is obtained to find the powers of the matrices satisfying the condition above via -Fibonacci numbers. Then, new properties related to -Fibonacci numbers are given. Moreover, some relations between the sequence and the generalized Fibonacci sequence are also examined.

Keywords

• Generalized Fibonacci numbers
• (k,p)-Fibonacci numbers
• Matrices

2020 Mathematics Subject Classification

• 11B37
• 11B39
• 11B83

References

1. Anđelic, M., da Fonseca, C. M., & Yılmaz, F. (2022). The bi-periodic Horadam sequence and some perturbed tridiagonal 2-Toeplitz matrices: A unified approach. Heliyon, 8(2), Article ID e08863.
2. Bednarz, N. (2021). On (k, p)-Fibonacci numbers. Mathematics, 9(7), Article ID 727.
3. Du, Z., & da Fonseca, C. M. (2023). Root location for the characteristic polynomial of a Fibonacci type sequence. Czechoslovak Mathematical Journal, 73, 189–195.
4. Horadam, A. F. (1965). Generating functions for powers of a certain generalized sequence of numbers. Duke Mathematical Journal, 32(3), 437–446.
5. Horadam, A. F. (1965). Basic properties of a certain generalized sequence of numbers. The Fibonacci Quarterly, 3(3), 161–176.
6. Kalman, D., & Mena, R. (2003). The Fibonacci numbers—exposed. Mathematics Magazine, 76(3), 167–181.
7. Keskin, R., & Demirtürk, B. (2010). Some new Fibonacci and Lucas identities by matrix methods. International Journal of Mathematical Education in Science and Technology, 41(3), 379–387.
8. Keskin, R., & Şiar, Z. (2019). Some new identities concerning the Horadam sequence and its companion sequence. Communications of the Korean Mathematical Society, 34(1), 1–16.
9. King, C. H. (1960). Some Properties of the Fibonacci Numbers. Master’s Thesis. San Jose State College.
10. Özdemir, H., Karakaya, S., & Petik, T. (2021). On some 3 × 3 dimensional matrices associated with generalized Fibonacci numbers. Notes on Number Theory and Discrete Mathematics, 27(3), 63–72.
11. Paja, N., & Włoch, I. (2021). Some interpretations of the (k, p)-Fibonacci numbers. Commentationes Mathematicae Universitatis Carolinae, 62(3), 297–307.
12. Ribenboim, P. (2000). My Numbers, My Friend: Popular Lectures on Number Theory. Springer-Verlag Inc., New York.
13. Şiar, Z., & Keskin, R. (2013). Some new identities concerning generalized Fibonacci and Lucas numbers. Hacettepe Journal of Mathematics and Statistics, 42(3), 211–222.
14. Trojovsky, P. (2021). On the characteristic polynomial of (k, p)-Fibonacci sequence. Advances in Difference Equations, 28, Article ID 2021:28.
15. Udrea, G. (1996). A note on the sequence 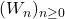of A. F. Horadam. Portugaliae Mathematica, 53(2), 143–155

Manuscript history

• Received: 6 June 2024
• Revised: 28 October 2024
• Accepted: 1 November 2024
• Online First: 8 November 2024

Copyright information

Ⓒ 2024 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).