Yagub N. Aliyev
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 3, Pages 474–485
DOI: 10.7546/nntdm.2023.29.3.474-485
Full paper (PDF, 790 Kb)
Details
Authors and affiliations
Yagub N. Aliyev ![]()
![]()
School of IT and Engineering, ADA University
Ahmadbey Aghaoglu str. 61, Baku, AZ1008, Azerbaijan
Abstract
We study the digits of the powers of 2 in the ternary number system. We propose an algorithm for doubling numbers in ternary numeral system. Using this algorithm, we explain the appearance of “stairs” formed by 0s and 2s when the numbers ![]() are written vertically so that for example the last digits are forming one column, the second last digits are forming another column, and so forth. We use the patterns formed by the leftmost digits, and the patterns formed by the rightmost digits to prove that the sizes of these blocks of 0s and 2s are unbounded. We also study how this regularity changes when the digits are taken between the left end and the right end of the numbers.
are written vertically so that for example the last digits are forming one column, the second last digits are forming another column, and so forth. We use the patterns formed by the leftmost digits, and the patterns formed by the rightmost digits to prove that the sizes of these blocks of 0s and 2s are unbounded. We also study how this regularity changes when the digits are taken between the left end and the right end of the numbers.
Keywords
- Ternary numeral system
- Benford’s law
- Digits
- Zeros
- Twos
- Powers of two
2020 Mathematics Subject Classification
- Primary: 11A63
- Secondary: 11A07, 11B83
References
- Benford, F. (1938). The law of anomalous numbers. Proceedings of the American Philosophical Society, 78(4), 551–572.
- Birkhoff, G. D. (1931). Proof of the ergodic theorem, Proceedings of the National Academy of Sciences USA, 17, 656–660.
- Bohl, P. (1909). Über ein in der Theorie der säkutaren Störungen vorkommendes Problem, Journal für die reine und angewandte Mathematik, 135, 189–283.
- Chang, S. (2023). Unlikely leading digits of powers of 2. Elemente der Mathematik, 78(2), 77–81.
- Erdős, P. (1979). Some unconventional problems in number theory. Mathematics Magazine, 52(2), 67–70.
- Erdős, P., & Graham, R. L. (1980). Old and New Problems and Results in Combinatorial Number Theory. Geneva, Switzerland: L’Enseignement Mathématique Université de Genève, Vol. 28.
- Hill, T. (1995). A statistical derivation of the significant-digit law. Statistical Science, 10(4), 354–363.
- Hill, T.P. (1995). The significant-digit phenomenon. The American Mathematical Monthly, 102(4) 322–327.
- Khintchine, A. (1933). Zu Birkhoffs Lösung des Ergodenproblems. Mathematische Annalen, 107, 485–488.
- Klenke, A. (2020). Probability Theory, A Comprehensive Course, Universitext, 716 p.
- Kuipers, L., & Niederreiter, H. (1974). Uniform Distribution of Sequences. John Wiley; Russian translation: Nauka, 1985.
- Lagarias, J. C. (2009). Ternary expansions of powers of 2. Journal of the London Mathematical Society, 79, 562–588.
- Origlio, V., & Weisstein, E.W. Ternary. From MathWorld – A Wolfram Web Resource, Available online at: https://mathworld.wolfram.com/Ternary.html
- Rosen, K. H. (2000). Elementary Number Theory and its Applicatons (4th ed.). Addison-Wesley-Longman.
- Sierpinski, W. (1910). Sur la valeur asymptotique d’une certaine somme. Bulletin International de l’Academie Polonaise des Sciences et des Lettres (Cracovie) series A, 9–11.
- Sloane, N. J. A. (1973). The persistence of a number. Journal of Recreational Mathematics, 6(2), 97–98.
- Sloane, N. J. A. (ed.), Powers of 2 written in base 3, The On-Line Encyclopedia of Integer Sequences (OEIS), A004642. Available online at: https://oeis.org/A004642
- Sobol, I. M. (1985). Points uniformly filling a high-dimensional cube. Znaniye, Mathematics, Cybernetics series, 2, 1–32 (in Russian).
- Strzelecki, P. (2004). On powers of 2. EMS Newsletter, 52, 7–8; translated from Polish journal Delta 7 (1994).
- Vardi, I. (1991). Computational Recreations in Mathematica. Reading, MA: Addison-Wesley.
- Weyl, H. (1910). Über die Gibbs’sche Erscheinung und verwandte Konvergenzphänomene. Rendiconti del Circolo Matematico di Palermo, 330, 377–407.
- Weyl, H. (1916). Über die Gleichverteilung von Zahlen mod. Eins. Mathematische Annalen, 77, 313–352.
Manuscript history
- Received: 23 November 2022
- Revised: 22 June 2023
- Accepted: 27 June 2023
- Online First: 10 July 2023
- Correction Notice: 24 July 2023Per Author’s request made on 23 July 2023, the following correction is made on page 474, line -7 of the Online First (electronic) version:
Old: In 1979, Paul Erdős conjectured that there are only finitely many positive integers that can be written as sum of distinct powers of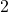 .
.
New: In 1979, Paul Erdős conjectured that there are only finitely many positive integers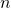 such that
such that 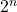 can be written as sum of distinct powers of
can be written as sum of distinct powers of 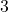 .
.
Copyright information
![]() Ⓒ 2023 by the Author.
Ⓒ 2023 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Aliyev, Y. N. (2023). Digits of powers of 2 in ternary numeral system. Notes on Number Theory and Discrete Mathematics, 29(3), 474-485, DOI: 10.7546/nntdm.2023.29.3.474-485.


