Number of stable digits of any integer tetration

Marco Ripà and Luca Onnis
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 28, 2022, Number 3, Pages 441–457
DOI: 10.7546/nntdm.2022.28.3.441-457
Full paper (PDF, 1147 Kb)

Details

Authors and affiliations

Marco Ripà
sPIqr Society, World Intelligence Network
Rome, Italy

Luca Onnis
Independent researcher
Cagliari, Italy

Abstract

In the present paper we provide a formula that allows to compute the number of stable digits of any integer tetration base a \in {\mathbb N}_0. The number of stable digits, at the given height of the power tower, indicates how many of the last digits of the (generic) tetration are frozen. Our formula is exact for every tetration base which is not coprime to 10, although a maximum gap equal to V(a)+1 digits (where V(a) denotes the constant congruence speed of a) can occur, in the worst-case scenario, between the upper and lower bound. In addition, for every a>1 which is not a multiple of 10, we show that V(a) corresponds to the 2-adic or 5-adic valuation of a-1 or a+1, or even to the 5-adic order of a^2+1, depending on the congruence class of a modulo 20.

Keywords

  • Tetration
  • Exponentiation
  • Congruence speed
  • Modular arithmetic
  • Stable digits
  • p-adic valuation

2020 Mathematics Subject Classification

  • 11A07
  • 11A15

References

  1. Cassels, J. W. S. (1986). Local Fields. London Mathematical Society Student Texts 3, Cambridge University Press, Cambridge.
  2. Daccache, G. (2015). Climbing the ladder of hyper operators: Tetration, Mathemathics Stack Exchange, Available online at:  https://math.blogoverflow.com/2015/01/05/climbing-the-ladder-of-hyper-operators-tetration/
  3. Germain, J. (2009). On the Equation 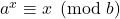a^x \equiv x \pmod b. Integers, 9(6), 629–638.
  4. Googology Wiki contributors (2021). Tetration. In Hyper operators, Googology Wiki | Fandom (Updated on Dec. 13 2021), Accessed: Dec. 27 2021, Available online at: https://googology.wikia.org/wiki/Tetration
  5. Hittmeir, M. (2020). A Reduction of Integer Factorization to Modular Tetration. International Journal of Foundations of Computer Sciences, 31(4), 461–481.
  6. OEIS Foundation Inc. (2022). The Online Encyclopedia of Integer Sequences, A063006. Accessed: Jan. 25 2022, Available online at: http://oeis.org/A063006
  7. Onnis, L. (2021). Observations regarding the repetitions of the last digits of a tetration of a generic base [v2], arXiv, 29 Sep. 2021. arXiv:2109.13679v2.
  8. Pr∞fWiki Contributors (2022). P-adic Valuation is Valuation, Pr∞fWiki (Updated on 16 Oct. 2021), Available online at: https://proofwiki.org/wiki/P-adic_Valuation_is_Valuation
  9. Quick, L. (2020). p-adic Absolute Values. The University of Chicago Mathematics REU 2020, Accessed: Feb 2. 2022, Available online at: https://math.uchicago.edu/~may/REU2020/REUPapers/Quick.pdf
  10. Ripà, M. (2011). La strana coda della serie n^n^…^n, UNI Service, Trento.
  11. Ripà, M. (2020). On the congruence speed of tetration. Notes on Number Theory and Discrete Mathematics, 26(3), 245–260.
  12. Ripà, M. (2021). The congruence speed formula. Notes on Number Theory and Discrete Mathematics, 27(4), 43–61.
  13. Urroz, J. J., & Yebra J. L. A. (2009). On the Equation 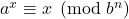a^x \equiv x \pmod {b^n}. Journal of Integer Sequences, 8(8), 1–8.

Manuscript history

  • Received: 16 February 2022
  • Revised: 29 June 2022
  • Accepted: 21 July 2022
  • Online First: 24 July 2022

Related papers

  1. Vassilev-Missana, M. (2010). Some results on infinite power towers. Notes on Number Theory and Discrete Mathematics, 16(3), 18-24.
  2. Ripà, M. (2020). On the constant congruence speed of tetration, Notes on Number Theory and Discrete Mathematics, 26(3), 245–260.
  3. Ripà, M. (2021). The congruence speed formula. Notes on Number Theory and Discrete Mathematics, 27(4), 43-61.

Cite this paper

Ripà, M., & Onnis, L. (2022). Number of stable digits of any integer tetration. Notes on Number Theory and Discrete Mathematics, 28(3), 441-457, DOI: 10.7546/nntdm.2022.28.3.441-457.

Comments are closed.