Volume 23 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
A note on the quartic Diophantine equation A4 + hB4 = C4 + hD4
Original research paper. Pages 1–3
Ajai Choudhry
Full paper (PDF, 113 Kb) | Abstract
Integer solutions of the diophantine equation A4 + hB4 = C4 + hD4 are known for all positive integer values of h < 1000. While a solution of the aforementioned diophantine equation for any arbitrary positive integer value of h is not known, Gerardin and Piezas found solutions of this equation when h is given by polynomials of degrees 5 and 2, respectively. In this paper, we present several new solutions of this equation when h is given by polynomials of degrees 2, 3 and 4.
Refinements of the Mitrinović–Adamović inequality, with application
Original research paper. Pages 4–6
József Sándor
Full paper (PDF, 139 Kb) | Abstract
We point out refinement of the Mitrinović–Adamović inequality, and offer an application to the new poof of a recent result.
New theorems on explicit evaluation of a parameter of Ramanujan’s χ(q) function
Original research paper. Pages 7–18
Nipen Saikia and Jubaraj Chetry
Full paper (PDF, 184 Kb) | Abstract
We prove many new theorems for the explicit values of the parameter Ik,n, for positive real number n and k, involving Ramanujan’s χ(q) function by establishing its connection with some other parameters of Ramanujan’s theta-functions. As applications of the parameter Ik,n we offer formulas for the explicit values of Ramanujan’s cubic continued fraction and χ(e−πn).
Inequalities for φ and ψ functions (III)
Original research paper. Pages 19–23
Krassimir T. Atanassov
Full paper (PDF, 148 Kb) | Abstract
A new arithmetic function is defined and some of its properties are studied.
Ascending sequences with neighboring elements add up to perfect square numbers
Original research paper. Pages 24–27
Kai Jin
Full paper (PDF, 128 Kb) | Abstract
We consider the problem of partitioning the numbers 1..
n to ascending sequences as few as possible, so that every neighboring pair of elements in each sequence add up to some perfect square number. We prove that the minimum number of sequences is
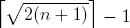
. We hope that this paper exhibits an interesting property of the perfect square numbers.
Some enumerations of non-trivial composition of the differential operations and the directional derivative
Original research paper. Pages 28–38
Ivana Jovović and Branko Malešević
Full paper (PDF, 179 Kb) | Abstract
This paper deals with some enumerations of the higher order non-trivial compositions of the differential operations and the directional derivative in the space ℝn (n ≥ 3). One new enumeration of the higher order non-trivial compositions is obtained.
Further results on arctangent sums with applications to generalized Fibonacci numbers
Original research paper. Pages 39–53
Robert Frontczak
Full paper (PDF, 206 Kb) | Abstract
In this article, we extend a classical trigonometric addition formula for the arctangent function and derive new summation identities for Fibonacci and Lucas numbers. While most of the results seem to be new, we also recover some known expressions.
Primitive Pythagorean triples and generalized Fibonacci sequences
Original research paper. Pages 54–62
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 206 Kb) | Abstract
It is proved that infinite sequences of generalized Fibonacci sequences obtained from generalizations of the Golden Ratio can generate all primitive Pythagorean triples. This is a consequence of the integer structure since the major component of a primitive Pythagorean triple always has the form (4r1 + 1) where r1 belongs to the class in the modular ring Z4.
Some combinatorial formulas for the partial r-Bell polynomials
Original research paper. Pages 63–76
Mark Shattuck
Full paper (PDF, 208 Kb) | Abstract
The partial r-Bell polynomials generalize the classical partial Bell polynomials (coinciding with them when r = 0) by assigning a possibly different set of weights to the blocks containing the r smallest elements of a partition no two of which are allowed to belong to the same block. In this paper, we study the partial r-Bell polynomials from a combinatorial standpoint and derive several new formulas. We prove some general identities valid for arbitrary values of the parameters as well as establish formulas for some specific evaluations. Several of our results extend known formulas for the partial Bell polynomials and reduce to them when r = 0. Our arguments are largely combinatorial, and therefore provide, alternatively, bijective proofs of these formulas, many of which were shown by algebraic methods.
An elementary alternative proof for Chan’s analogue of Ramanujan’s most beautiful identity and some inequality of the cubic partition
Original research paper. Pages 77–87
Koustav Banerjee and Prabir Das Adhikary
Full paper (PDF, 193 Kb) | Abstract
In this paper we provide an alterative proof for the congruence modulo 3 of the cubic partition a(n). That apart we also examine inequalities a(n) and provide upper bound for it in the fashion of the classic partition function p(n).
A Fibonacci integral lattice approach to Pythagoras’ Theorem
Original research paper. Pages 88–90
Anthony G. Shannon and John N. Crothers
Full paper (PDF, 55 Kb) | Abstract
Square integral lattices with basis vector pairs {(a, b), (b, –a)}, where a and b are successive Fibonacci numbers, are employed to develop intermediate convergence forms of Pythagoras’ Theorem for triangles with integral sides.
On the bounds for the norms of circulant matrices with the Jacobsthal and Jacobsthal–Lucas numbers
Original research paper. Pages 91–98
Ş. Uygun and S. Yaşamalı
Full paper (PDF, 175 Kb) | Abstract
In this study, we have found upper and lower bounds for the spectral norms of circulant matrices in the forms A = Cr(j0, j1, …, jn−1) and B = Cr(c0, c1, …, cn−1).
A note on the density of quotients of primes in arithmetic progressions
Original research paper. Pages 99–100
Brian D. Sittinger
Full paper (PDF, 133 Kb) | Abstract
We give an alternate proof to the density of quotients of primes in an arithmetic progression which has been established by Micholson [2] and Starni [4].
On some cancellation algorithms
Original research paper. Pages 101–114
Andrzej Tomski and Maciej Zakarczemny
Full paper (PDF, 224 Kb) | Abstract
Let f be a natural-valued function defined on the Cartesian product of finitely many copies of ℕ (positive integers). Here we will discuss some modifications of the sieve of Eratosthenes in the sense that we cancel the divisors of all possible values of f in the points whose sum of coordinates is less or equal to n. By applying similar arguments to those used in the paper (J. Browkin, H-Q. Cao, Modifications of the Eratosthenes sieve, Colloq. Math. 135, (2014)), but also in the companion papers, we investigate new problems for the values of some polynomial functions or quadratic and cubic forms.
Volume 23 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
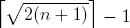 . We hope that this paper exhibits an interesting property of the perfect square numbers.
. We hope that this paper exhibits an interesting property of the perfect square numbers.


