Ascending sequences with neighboring elements add up to perfect square numbers

Kai Jin
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 23, 2017, Number 1, Pages 24–27
Full paper (PDF, 128 Kb)

Details

Authors and affiliations

Kai Jin
Institute for Interdisciplinary Information Sciences
Tsinghua University
Beijing 100084, China

Abstract

We consider the problem of partitioning the numbers 1..n to ascending sequences as few as possible, so that every neighboring pair of elements in each sequence add up to some perfect square number. We prove that the minimum number of sequences is 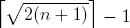. We hope that this paper exhibits an interesting property of the perfect square numbers.

Keywords

• Perfect square number
• Elementary Number theory
• Sequences

AMS Classification

• 11B75
• 11B83

References

1. Anonymous, Arranging numbers from 1 to n such that the sum of every two adjacent numbers is a perfect power, www.mathoverflow.net, 2015, http://mathoverflow.net/questions/199677/.
2. Anonymous, Problems & Puzzles: Puzzle 311. Sum to a cube, www.primepuzzles.net, http://www.primepuzzles.net/puzzles/puzz_311.htm.