Volume 22 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
The definitive solution of Gauss’s lattice points problem in the circle
Original research paper. Pages 1–3
Aldo Peretti
Full paper (PDF, 464 Kb) | Abstract
By means of Bienayme’s theorem of Statistics is found that the remainder term in Gauss’s problem about the lattice points in the circle is a function normally distributed with mean value zero and standard deviation 1,10368 multiplied by the fourth root of x. This result can not be improved.
On irrationality of some distances between points on a circle
Original research paper. Pages 4–9
Mladen Vassilev–Missana
Full paper (PDF, 155 Kb) | Abstract
Let
n > 3 be arbitrary integer. In the present paper it is shown that if
K is an arbitrary circle and
Mi,
i = 1,…,
n are points on
K, dividing
K into
n equal arcs, then for each point
M on
K, different from the mentioned above, at least
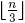
of the distances |
MMi| are irrational numbers.
Catalan triangles and Finucan’s hidden folders
Original research paper. Pages 10–16
A. G. Shannon
Full paper (PDF, 138 Kb) | Abstract
This note is to capture and extend some of Finucan’s ideas for further exploration by students. These ideas connect with several elementary concepts in combinatorial analysis which lend themselves to undergraduate research projects
On function “Restrictive factor”
Original research paper. Pages 17–22
Krassimir T. Atanassov
Full paper (PDF, 172 Kb) | Abstract
Some new properties of the arithmetic function called “Restrictive factor” are formulated and studied.
On transitive polynomials modulo integers
Original research paper. Pages 23–35
Mohammad Javaheri and Gili Rusak
Full paper (PDF, 223 Kb) | Abstract
A polynomial P(x) with integer coefficients is said to be transitive modulo m, if for every x, y ∈ ℤ there exists k ≥ 0 such that Pk(x) = y (mod m). In this paper, we construct new examples of transitive polynomials modulo prime powers and partially describe cubic and quartic transitive polynomials. We also study the orbit structure of affine maps modulo prime powers.
The n × n × n Points Problem optimal solution
Original research paper. Pages 36–43
Marco Ripà
Full paper (PDF, 557 Kb) | Abstract
We provide an optimal strategy to solve the n × n × n points problem inside the box, considering only 90° turns, and at the same time a pattern able to drastically lower down the known upper bound. We use a very simple spiral frame, especially if compared to the previous plane by plane approach that significantly reduces the number of straight lines connected at their end-points necessary to join all the n3 dots. In the end, we combine the square spiral frame with the rectangular spiral pattern in the most profitable way, in order to minimize the difference hu(n) − hl(n) between the upper and the lower bound, proving that it is ≤ 0.5 ∙ n ∙ (n + 3), for any n > 1.
Maximal trees with log-concave independence polynomials
Original research paper. Pages 44–53
Eugen Mandrescu and Alexander Spivak
Full paper (PDF, 182 Kb) | Abstract
If
sk denotes the number of independent sets of cardinality
k in graph
G, and
α(
G) is the size of a maximum independent set, then
![Rendered by QuickLaTeX.com \[ I(G;x)=\sum_{k=0}^{\alpha(G)}s_k x^k \]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-93ce5be532cb40451f6a2a83fe3e60fa_l3.png)
is the independence polynomial of G (I. Gutman and F. Harary, 1983, [8]). The Merrifield–Simmons index σ(G) (known also as the Fibonacci number) of a graph G is defined as the number of all independent sets of G. Y. Alavi, P. J. Malde, A. J. Schwenk and P. Erdos (1987, [2]) conjectured that I(T,x) is unimodal whenever T is a tree, while, in general, they proved that for each permutation π of {1, 2, …, α} there is a graph G with α(G) = α such that sπ(1) < sπ(2) < … < sπ(α). By maximal tree on n vertices we mean a tree having a maximum number of maximal independent sets among all the trees of order n. B. Sagan proved that there are three types of maximal trees, which he called batons [24].
In this paper we derive closed formulas for the independence polynomials and Merrifield–Simmons indices of all the batons. In addition, we prove that I(T,x) is log-concave for every maximal tree T having an odd number of vertices. Our findings give support to the above mentioned conjecture.
Series expansions related to the logarithmic mean
Original research paper. Pages 54–57
József Sándor
Full paper (PDF, 126 Kb) | Abstract
We show that the Gregory series combined with Newton’s binomial expansion give a natural approach to the logarithmic mean inequalities.
Sequences obtained from x2 ± y2
Original research paper. Pages 58–63
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 137 Kb) | Abstract
Integers in class ̅34 of the modular ring Z4 equal x2 – y2 but not x2 + y2 whereas integers in class ̅14 can equal both x2 + y2 and x2 – y2. This structure generates an infinity of sequences with neat curious patterns.
A note on a family of alternating Fibonacci sums
Original research paper. Pages 64–71
Robert Frontczak
Full paper (PDF, 167 Kb) | Abstract
In this note we consider a family of finite and infinite alternating sums containing products of Fibonacci numbers. We derive closed-form expressions for this family of sums. As a consequence of this result we establish new algebraic relationships between certain alternating sums of reciprocals of products of Fibonacci numbers with integer power.
On subgroups of non-commutative general rhotrix group
Original research paper. Pages 72–90
A. Mohammed and U. E. Okon
Full paper (PDF, 208 Kb) | Abstract
This paper considers the pair (GRn(F),⚬) consisting of the set of all invertible rhotrices of size n over an arbitrary field F; and together with the binary operation of row-column method for rhotrix multiplication; in order to introduce it as the concept of “non-commutative general rhotrix group”. We identify a number of subgroups of (GRn(F),⚬) and then advance to show that its particular subgroup is embedded in a particular subgroup of the well-known general linear group (GRn(F),•). Furthermore, we shall investigate isomorphic relationship between some subgroups of (GRn(F),⚬).
Volume 22 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
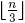 of the distances |MMi| are irrational numbers.
of the distances |MMi| are irrational numbers.
![Rendered by QuickLaTeX.com \[ I(G;x)=\sum_{k=0}^{\alpha(G)}s_k x^k \]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-93ce5be532cb40451f6a2a83fe3e60fa_l3.png)


