A. M. S. Ramasamy
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 30, 2024, Number 1, Pages 116–140
DOI: 10.7546/nntdm.2024.30.1.116-140
Full paper (PDF, 347 Kb)
Details
Authors and affiliations
A. M. S. Ramasamy ![]()
![]()
Department of Mathematics, Pondicherry University
Pondicherry – 605014, India
Abstract
The aim of this work is to present a method using the cyclic sequences ![]() and
and ![]() in the finite fields
in the finite fields ![]() , with
, with ![]() a prime, that yield divisors of Mersenne, Fermat and Lehmer numbers. The transformations
a prime, that yield divisors of Mersenne, Fermat and Lehmer numbers. The transformations ![]() and
and ![]() are introduced which lead to the proof of the cyclic nature of the sequences
are introduced which lead to the proof of the cyclic nature of the sequences ![]() and
and ![]() . Results on the roots of the
. Results on the roots of the ![]() -polynomials in
-polynomials in ![]() form the central theme of the study.
form the central theme of the study.
Keywords
- Satellite polynomials
- M-cycle
- Background prime
- The transformations
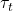 and
and 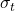
- Symmetric and skew-symmetric properties
- Pivotal elements
- Euler’s totient function
2020 Mathematics Subject Classification
- 11A51
- 11B50
- 11C08
- 11T06
References
- Brillhart, J. (1964). On the factors of certain Mersenne numbers II. Mathematics of Computation, 18, 87–92.
- Brillhart, J., & Johnson, G. D. (1960). On the factors of certain Mersenne numbers. Mathematics of Computation, 14, 365–369.
- Hardy, G. H., & Wright, E. M. (1971). An Introduction to the Theory of Numbers. (4th ed.). The English Language Book Society.
- Kang, S. W. (1989). On the primality of the Mersenne number Mp. Journal of the Korean Mathematical Society, 26(1), 75–82.
- Kravitz, S. (1961). Divisors of Mersenne numbers 10, 000 < p < 15, 000. Mathematics of Computation, 15, 292–293.
- Leyendekkers, J. V., & Shannon, A. G. (2005). Fermat and Mersenne numbers. Notes on Number Theory and Discrete Mathematics, 11(4), 17–24.
- Mohanty, S. P., & Ramasamy, A. M. S. (1985). The characteristic number of two simultaneous Pell’s equations and its application. Bulletin of the Belgian Mathematical Society – Simon Stevin, 59(2), 203–214.
- Ramasamy, A. M. S. (2006). Generalized version of the characteristic number of two simultaneous Pell’s equations. The Rocky Mountain Journal of Mathematics, 36(2), 699–720.
- Ribenboim, P. (1996). The New Book of Prime Number Records. Springer–Verlag.
Manuscript history
- Received: 25 August 2023
- Revised: 4 March 2024
- Accepted: 6 March 2024
- Online First: 7 March 2024
Copyright information
![]() Ⓒ 2024 by the Author.
Ⓒ 2024 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
- Leyendekkers, J. V., & Shannon, A. G. (2005). Fermat and Mersenne numbers. Notes on Number Theory and Discrete Mathematics, 11(4), 17–24.
- Ramasamy, A. M. S. (2024). Sequences in finite fields yielding divisors of Mersenne, Fermat and Lehmer numbers, II. Notes on Number Theory and Discrete Mathematics, 30(2), 236-252.
- Ramasamy, A. M. S. (2024). Partitions of numbers and the algebraic principle of Mersenne, Fermat and even perfect numbers. Notes on Number Theory and Discrete Mathematics, 30(4), 755-775.
Cite this paper
Ramasamy, A. M. S. (2024). Sequences in finite fields yielding divisors of Mersenne, Fermat and Lehmer numbers, I. Notes on Number Theory and Discrete Mathematics, 30(1), 116-140, DOI: 10.7546/nntdm.2024.30.1.116-140.


