J. V. Leyendekkers and A. G. Shannon
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 11, 2005, Number 4, Pages 17–24
Full paper (PDF, 114 Kb)
Details
Authors and affiliations
J. V. Leyendekkers
The University of Sydney, 2006 Australia
A. G. Shannon
Warrane College, Kensington, NSW 1465,
& KvB Institute of Technology, North Sydney, NSW 2060, Australia
Abstract
Fermat numbers (Fn = 22n + 1) and Mersenne numbers (Mm = 2m − 1), m odd, are compared on the basis of integer structure, using the modular rings Z4 and Z6. The two numbers fall in different classes and this results in different composite row structures and different potentials for the formation of primes. The constraints on 2n and the right end digits for Fn result in fewer numbers over a given range than those for Mm. This is shown with two functions, which link the two numbers and show that Fn = (2x2 + y2 − 1 + 1): for primes y = n, but when n > 4, y ≠ n.
AMS Classification
- 11A41
- 11A07
References
- Krassimir T Atanassov, A Relation between the Prime and the Fibonacci Numbers, Advanced Studies in Contemporary Mathematics, 6(1) (2003): 53-56.
- John Brillhart, D.H. Lehmer, J.L. Selfridge, Bryant Tuckerman & S.S. Wagstaff Jr, Factorization of bn ±1, b = 2,3,5,6,7,10,11,12 up to High Powers. 2nd Edition. Providence, RI: American Mathematical Society, 1988.
- Graeme L. Cohen, On a Conjecture of Mạkowski and Schinzel. Colloquium Mathematicum, 74(1) (1997): 1-8.
- B. Ghusayni, Maple Explorations, Perfect Numbers, and Mersenne Primes. International Journal of Mathematical Education in Science and Technology,36 (6) (2005): 643-654.
- G.H. Hardy & E.M. Wright, An Introduction to the Theory of Numbers. Oxford: Clarendon Press, 1945, p.14.
- J.V. Leyendekkers, J.M. Rybak & A.G. Shannon, Integer Class Properties Associated with an Integer Matrix. Notes on Number Theory & Discrete Mathematics. 1 (2) (1995): 53-59.
- J.V. Leyendekkers, J.M. Rybak & A.G. Shannon, Analysis of Diophantine Properties Using Modular Rings with Four and Six Classes. Notes on Number Theory & Discrete Mathematics. 3 (2) (1997): 61-74.
- J.V. Leyendekkers, J.M. Rybak & A.G. Shannon, The Characteristics of Primes and Other Integers within the Modular Ring Z4 and in Class
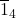 . Notes on Number Theory & Discrete Mathematics. 4 (1) (1998): 1-17.
. Notes on Number Theory & Discrete Mathematics. 4 (1) (1998): 1-17. - J.V. Leyendekkers & A.G. Shannon, Expansion of Integer Powers from Fibonacci’s Odd Number Triangle. Notes on Number Theory & Discrete Mathematics. 7(2) 2001: 48-59.
- J.V. Leyendekkers & A.G. Shannon, The Analysis of Twin Primes within Z6. Notes on Number Theory & Discrete Mathematics. 7(4) 2001: 115-124.
- J.V. Leyendekkers & A.G. Shannon, Fermat’s Theorem on Binary Powers, Notes on Number Theory & Discrete Mathematics. Vol. 11, 2005, No. 2, 13-22..
- Hans Riesel. Prime Numbers and Computer Methods for Factorization. 2nd edition. Progress in Mathematics, Volume 126. Boston: Birkhäuser, 1994.
- W.W. Rouse Ball (revised by H.S.M. Coxeter), Mathematical Recreations and Essays. 11th Edition. London: Macmillan, 1956.
Related papers
- Ramasamy, A. M. S. (2024). Sequences in finite fields yielding divisors of Mersenne, Fermat and Lehmer numbers, I. Notes on Number Theory and Discrete Mathematics, 30(1), 116-140.
Cite this paper
Leyendekkers, J. V., & Shannon, A. G. (2005). Fermat and Mersenne numbers. Notes on Number Theory and Discrete Mathematics, 11(4), 17-24.


