R. K. Davala
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 3, Pages 495–502
DOI: 10.7546/nntdm.2023.29.3.495-502
Full paper (PDF, 222 Kb)
Details
Authors and affiliations
R. K. Davala ![]()
![]()
VIT-AP University, Amaravati, Andhra Pradesh, India
Abstract
Let ![]() and
and ![]() be the
be the ![]() -th balancing and Lucas-balancing numbers, respectively. We consider the Diophantine equations
-th balancing and Lucas-balancing numbers, respectively. We consider the Diophantine equations ![]() and
and ![]() for
for ![]()
![]()
![]() and present the non-negative integer solutions of the Diophantine equations in each case.
and present the non-negative integer solutions of the Diophantine equations in each case.
Keywords
- Balancing numbers
- Lucas-balancing numbers
- Diophantine equation
2020 Mathematics Subject Classification
- 11B39
- 11B37
References
- Behera, A., & Panda, G. K. (1999). On the square roots of triangular numbers. The Fibonacci Quarterly, 37(2), 98–105.
- Beiter, M. (1964). The midterm coefficient of the cyclotomic polynomial
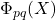 . American Mathematical Monthly, 71, 769–770.
. American Mathematical Monthly, 71, 769–770. - Chu, H. V. (2020). Representation of
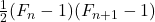 and
and 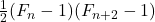 . The Fibonacci Quarterly, 58(4), 334–339.
. The Fibonacci Quarterly, 58(4), 334–339. - Davala, R. K. (2015). On convolution and binomial sums of balancing and Lucas-balancing numbers. International Journal of Mathematical Sciences and Engineering Applications, 8(5), 77–83.
- Davala, R. K. (2018). Algebraic and geometric aspects of some binary recurrence
sequences. Ph.D. Thesis, National Institute of Technology, Rourkela, India. - Davala, R. K., & Panda, G. K. (2015). On sum and ratio formulas for balancing numbers. The Journal of the Indian Mathematical Society, 82(2), 23–32.
- Davala, R. K., & Panda, G. K. (2016). On sum and ratio formulas for balancing-like sequences. Notes on Number Theory and Discrete Mathematics, 22(3), 45–53.
- Davala, R. K., & Panda, G. K. (2019). On sum and ratio formulas for Lucas-balancing numbers. Palestine Journal of Mathematics, 8(2), 200–206.
- Frontczak, R. (2018). Sums of balancing and Lucas-balancing numbers with binomial coefficients. International Journal of Mathematical Analysis, 12, 585–594.
- Panda, G. K. (2009). Some fascinating properties of balancing numbers. Congressus Numerantium, 194, 265–271.
- Ray, P. K. (2009). Balancing and cobalancing numbers. Ph.D. Thesis, National Institute of Technology, Rourkela, India.
- Ray, P. K. (2015). Balancing and Lucas-balancing sums by matrix methods. Mathematical Reports, 17(2), 225–233.
- Soykan, Y. (2021). A study on generalized balancing numbers. Asian Journal of Advanced Research and Reports, 15(5), 78–100.
Manuscript history
- Received: 10 March 2023
- Revised: 28 June 2023
- Accepted: 13 July 2023
- Online First: 15 July 2023
Copyright information
![]() Ⓒ 2023 by the Author.
Ⓒ 2023 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
- Davala, R. K., & Panda, G. K. (2016). On sum and ratio formulas for balancing-like sequences. Notes on Number Theory and Discrete Mathematics, 22(3), 45–53.
Cite this paper
Davala, R. K. (2023). Solution to a pair of linear, two-variable, Diophantine equations with coprime coefficients from balancing and Lucas-balancing numbers. Notes on Number Theory and Discrete Mathematics, 29(3), 495-502, DOI: 10.7546/nntdm.2023.29.3.495-502.


