Anier Soria-Lorente and Stefan Berres
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 26, 2020, Number 3, Pages 107–134
DOI: 10.7546/nntdm.2020.26.3.107-134
Full paper (PDF, 324 Kb)
Details
Authors and affiliations
Anier Soria-Lorente ![]()
Department of Technology, University of Granma
Bayamo-Granam, Cuba
Stefan Berres ![]()
Departamento de Ciencias Matemáticas y Físicas, Facultad de Ingeniería
Universidad Católica de Temuco, Temuco, Chile
Abstract
Inspired by the results of Rhin and Viola (2001), the purpose of this work is to elaborate on a series representation for ζ(3) which only depends on one single integer parameter. This is accomplished by deducing a Hermite–Padé approximation problem using ideas of Sorokin (1998). As a consequence we get a new recurrence relation for the approximation of ζ(3) as well as a corresponding new continued fraction expansion for ζ(3), which do no reproduce Apéry’s phenomenon, i.e., though the approaches are different, they lead to the same sequence of Diophantine approximations to ζ(3). Finally, the convergence rates of several series representations of ζ(3) are compared.
Keywords
- Riemann zeta function
- Apéry’s theorem
- Hermite–Padé approximation problem
- Recurrence relation
- Continued fraction expansion
- Series representation
2010 Mathematics Subject Classification
- Primary
- 11B37
- 30B70
- 14G10
- 11J72
- 11M06
- Secondary
- 37B20
- 11A55
- 11J70
- 11Y55
- 11Y65
References
- Abramov, S. A. (2002). Applicability of Zeilberger’s algorithm to hypergeometric terms. In: Proceedings of the 2002 International Symposium on Symbolic and Algebraic Computation, 1-7.
- Abramov, S. A. (2003). When does Zeilberger’s algorithm succeed? Advances in Applied Mathematics, 30 (3), 424-441.
- Abramov, S. A., Carette, J. J., Geddes, K. O., & Le, H. Q. (2004). Telescoping in the context of symbolic summation in maple. J. of Symb. Comput, 38 (4), 1303-1326.
- Abramov, S. A., & Le, H.Q. (2002). A criterion for the applicability of Zeilberger’s algorithm to rational functions. Discrete Math. 259 (1-3), 1-17.
- Abramowitz, M., & Stegun, I.A. (1964). Handbook of mathematical functions: with formulas, graphs, and mathematical tables, Vol. 55. Courier Corporation.
- Alzer, H., Karayannakis, D., & Srivastava, H. M. (2006). Series representations for some mathematical constants. J. Math. Anal. Appl., 320 (1), 145-162.
- Amdeberhan, T.(1996). Faster and faster convergent series for
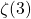 . Electron. J. Combin., 3 (1), R13.
. Electron. J. Combin., 3 (1), R13. - Amdeberhan, T., & Zeilberger, D. (1997). Hypergeometric series acceleration via the WZ method. Electron. J. Combin., 4 (2), R3.
- Apéry, R. (1979). Irrationalité de
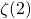 et
et 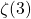 . Astérisque, 61, 11-13.
. Astérisque, 61, 11-13. - Arvesú , J., & Soria-Lorente, A. (2012). On new rational approximants to
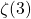 . arXiv preprint arXiv:1204.6712.
. arXiv preprint arXiv:1204.6712. - Balanzario, E. (2001). Método elemental para la evaluación de la función zeta de Riemann en los enteros pares. Miscelánea Mat, 33, 31-41.
- Ball, K., & Rivoal, T. (2001). Irrationalité d’une infinité de valeurs de la fonction zêta aux entiers impairs. Invent. Math., 146 (1), 193-207.
- Beukers, F. (1979). A note on the irrationality of
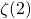 and
and 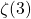 . Bull. London Math. Soc., 11 (13), 268-272.
. Bull. London Math. Soc., 11 (13), 268-272. - Beukers, F. (1980). Legendre polynomials in irrationality proofs. Bull. Austral. Math. Soc., 22 (3), 431-438.
- Beukers, F. (1980). Padé-approximations in number theory. Séminaire de Théorie des Nombres de Bordeaux, 1-9.
- Beukers, F. (2003). Consequences of Apéry’s work on
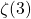 . Preprint of talk presented at the Rencontres Arithmétiques de Caen,
. Preprint of talk presented at the Rencontres Arithmétiques de Caen, , Irrationnel: Les Retombées.
, Irrationnel: Les Retombées. - Borwein, J. M., Bradley, D. M.,& Crandall, R. E. (2000). Computational strategies for the Riemann zeta function. J. Comput. Appl. Math., 121 (1-2), 247-296.
- Chen, M. P., & Srivastava, H. M. (1998). Some families of series representations for the Riemann
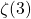 . Result. Math., 33 (3-4), 179-197.
. Result. Math., 33 (3-4), 179-197. - Cheng, H., Gergel, B., Kim, E., & Zima, E. (2005). Space-efficient evaluation of hypergeometric series. ACM SIGSAM Bulletin, 39 (2), 41-52.
- Cohen, H. (1978). Démonstration de l’irrationalité de
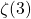 (d’apres Apéry).
(d’apres Apéry).
Séminaire de Théorie des Nombres, Grenoble. - Conway, J. H., & Guy, R. (2012). The Book of Numbers. Springer Science & Business Media.
- Dvornicich, R., & Viola, C. (1987). Some remarks on Beukers’ integrals. Colloq. Math. Soc. János Bolyai, 2 (1), 637-657.
- Elsner, C. (2008). On prime-detecting sequences from Apéry’s recurrence formulae for
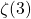 and
and 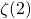 . J. Integer Seq., 11 (2), 3-21.
. J. Integer Seq., 11 (2), 3-21. - Fischler, S., Sprang, J., & Zudilin, V. (2019). Many odd zeta values are irrational. Compositio Mathematica, 155 (5), 938-952.
- Gasper, G., & Rahman, M. (2004). Basic hypergeometric series, Vol. 96. Cambridge University Press.
- Gutnik, L. (1983). On the irrationality of certain quantities involving
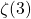 . Acta Arith., 42 (1), 255-264.
. Acta Arith., 42 (1), 255-264. - Hata, M. (1990). Legendre type polynomials and irrationality measures. J. Reine Angew. Math, 407 (1), 99-125.
- Hata, M. (1995). A note on Beukers’ integral. J. Austral. Math. Soc. Ser., 58 (2), 143-153.
- Hata, M. (2000). A new irrationality measure for
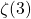 . Acta Arith., 92 (1), 47-57.
. Acta Arith., 92 (1), 47-57. - Janous, W.(2006). Around Apéry’s constant. J. Inequal. Pure Appl. Mah, 7 (1), Article 35.
- Jones, W. B., Thron, W. J., Browder, F.E., & Henrici, P. (1980). Continued fractions: Analytic theory and applications. Encyclopedia Math. Appl. Section: Analysis 11, Addison-Wesley, London.
- Kellerhals, R. (2012). Scissors congruence, the golden ratio and volumes in hyperbolic 5-space. Discrete & Computational Geometry, 47 (3), 629-658.
- Koekoek, R., Lesky, P. A., & Swarttouw, R. F. (2010). Hypergeometric orthogonal polynomials and their
 -analogues. Springer Science & Business Media.
-analogues. Springer Science & Business Media. - Kondratieva, M., & Sadov, S. (2005). Markov’s transformation of series and the WZ method. Advances in Applied Mathematics 34 (2), 393-407.
- Lagarias, J. (2013). Euler’s constant: Euler’s work and modern developments. Bulletin of the American Mathematical Society, 50 (4), 527-628.
- Lima, F. (2012). A simple approximate expression for the Apéry’s constant accurate to 21 digits. Preprint. Available online at: https://www.researchgate.net/publication/253390624.
- Luke, Y. L. (1969). Special functions and their approximations, Vol. 2. Academic Press, New York.
- Markov, A. A. (1890). Memoire sur la transformation des series peu convergentes en series tres convergentes. Par Andre Markoff. Mém. de l’Acad. Imp. Sci. de St. Pétersbourg, XXXVII (9), St. Pétersbourg, Eggers, 18 pages.
- Musha, T. (2014). Negation of the conjecture for odd zeta values. International Journal of Pure and Applied Mathematics, 91 (1), 103-111.
- Nesterenko, Y. V. (1996). A few remarks on
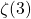 . Math. Notes, 59 (6), 625-636.
. Math. Notes, 59 (6), 625-636. - Nesterenko, Y. V. (2003). Integral identities and constructions of approximations to zeta values. J. Théor. Nombres Bordeaux, 15 (2), 535-550.
- Nesterenko, Y. V. (2009). An elementary proof of the irrationality of
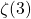 . Moscow Univ. Math. Bull., 64 (4), 165-171.
. Moscow Univ. Math. Bull., 64 (4), 165-171. - Nikiforov, A. F., & Uvarov, V.B. (1988) Special functions of mathematical physics, Birkhauser Basel.
- Perron, O. (1909). Über einen Satz des Herrn Poincaré. Journal für die reine und angewandte Mathematik 136, 17-37.
- Petkovšek, M., Wilf, H. S., & Zeilberger, D. (1996).
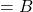 . A. K. Peters, Ltd., Wellesley, M.A. 30.
. A. K. Peters, Ltd., Wellesley, M.A. 30. - Pilehrood, K. H., & Pilehrood, T. H. (2008). Generating function identities for
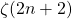 ,
, 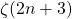 via the WZ method. Electron. J. Comb. 15 (1), 35-43.
via the WZ method. Electron. J. Comb. 15 (1), 35-43. - Pilehrood, K. H., & Pilehrood, T. H. (2008). Simultaneous generation for zeta values by the Markov-WZ method. Electron. J. Comb., 10 (3), 115-124.
- Pilehrood, K. H., & Pilehrood, T.H. (2010). Series acceleration formulae for beta values. Discrete Math. Theoret. Comput. Sci., 12 (2), 223-236.
- Poincaré, H. (1885). Sur les équations linéaires aux différentielles ordinaires et aux différences finies. Amer. J. Math., 7, 203-258.
- der Poorten, A. V. (1979). A proof that Euler missed… Apéry’s proof of the irrationality of
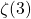 . Math. Intelligencer, 1, 195-203.
. Math. Intelligencer, 1, 195-203. - Prévost, M. (1996). A new proof of the irrationality of
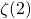 and
and 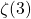 using Padé approximants.J. Comput. Appl. Math., 67 (2), 219-235.
using Padé approximants.J. Comput. Appl. Math., 67 (2), 219-235. - Rhin, G., & Viola, C. (1996). On a permutation group related to
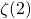 . Acta Arith. 77 (1), 23-56.
. Acta Arith. 77 (1), 23-56. - Rhin, G., & Viola, C. (2001). The group structure for
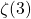 . Acta Arithmetica-Warszawa, 97 (3), 269-293.
. Acta Arithmetica-Warszawa, 97 (3), 269-293. - Rivoal, T. (2003). Séries hypergéométriques et irrationalité des valeurs de la fonction zêta de Riemann. J. Théor. Nombres Bordeaux 15(1), 351-365.
- Scheufens, E. E. (2013). Bernoulli polynomials, fourier series and zeta numbers. International Journal of Pure and Applied Mathematics, 88 (1), 65-75.
- Smet, C., & Van Assche, W. (2010). Mellin transforms for multiple Jacobi-Piñeiro polynomials and a
 -analogue. J. Approx. Theory, 162 (4), 782-806.
-analogue. J. Approx. Theory, 162 (4), 782-806. - Soria-Lorente, A. (2014). Arithmetic of the values of the Riemann’s zeta function in integer arguments. G.I.E Pensamiento Matemático, 4 (1), 33-44.
- Soria-Lorente, A. (2014). Nesterenko-like rational function, useful to prove the Apéry’s theorem. Notes Number Theory Discrete Math., 20 (2), 79-91.
- Soria-Lorente, A. (2018). On Zudilin-like rational approximations to ζ(5). Notes Number Theory Discrete Math., 24 (2), 104-116.
- Sorokin, V. N. (1994). Hermite–Padé approximations for Nikishin systems and the irrationality of
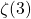 . Russian Mathematical Surveys, 49 (2), 176-177.
. Russian Mathematical Surveys, 49 (2), 176-177. - Sorokin, V. N. (1998). Apéry’s theorem. Vestnik Moskov. Univ. Ser. I Mat. Mekh. [Moscow Univ. Math. Bull.], 3, 48-52.
- Srivastava, H. M. (2000). Some simple algorithms for the evaluations and representations of the Riemann zeta function at positive integer arguments. J. Math. Anal. Appl., 246 (2), 331-351.
- Srivastava, H. M. (2015). Some properties and results involving the zeta and associated functions. Functional Analysis, Approximation and Computation, 7 (2), 89-133.
- Srivastava, H. M. (2000). Some families of rapidly convergent series representations for the zeta functions. Taiwanese Journal of Mathematics, 4 (4), 569-598.
- Van Assche, W. (1999). Multiple orthogonal polynomials, irrationality and transcendence. Contemp. Math., 236, 325-342.
- Van Assche, W. (2011). Hermite–Padé rational approximation to irrational numbers. Computational Methods and Function Theory, 10 (2), 585-602.
- Webster, J.B. (2008). Comparsion of two methods for modeling electron-radiation interactions, Undergraduate Honors Thesis, University of California, San Diego.
- Zudilin, V. (1997). Difference equations and the irrationality measure of numbers. Proc. Steklov Inst. Math., 218, 160-174.
- Zudilin, V. (2002). A third-order Apéry-like recursion for
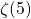 .Math. Notes, 72 (5–6), 733-737.
.Math. Notes, 72 (5–6), 733-737. - Zudilin, W. (2002). An elementary proof of Apéry’s theorem. arXiv preprint math/0202159.
- Zudilin, W. (2004). Arithmetic of linear forms involving odd zeta values. J. Théor. Nombres Bordeaux, 16 (1), 251-291.
- Zudilin, W. (2004). Well-poised hypergeometric transformations of Euler-type multiple integrals, J. London Math. Soc., 70 (1), 215-230.
Related papers
- Soria-Lorente, A. (2014). Nesterenko-like rational function, useful to prove the Apéry’s theorem. Notes on Number Theory and Discrete Mathematics, 20(2), 79-91.
- Soria-Lorente, A. (2018). On Zudilin-like rational approximations to ζ(5). Notes on Number Theory and Discrete Mathematics, 24(2), 104-116.
Cite this paper
Soria-Lorente, A., & Berres, S. (2020). A single parameter Hermite–Padé series representation for Apéry’s constant. Notes on Number Theory and Discrete Mathematics, 26 (3), 107-134, DOI: 10.7546/nntdm.2020.26.3.107-134.


