Divisibility and sequence properties of σ+ and φ+

Sagar Mandal
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 4, Pages 899–907
DOI: 10.7546/nntdm.2025.31.4.899-907
Full paper (PDF, 210 Kb)

Details

Authors and affiliations

Sagar Mandal
Department of Mathematics, Indian Institute of Technology Ropar
Punjab, India

Abstract

Inspired by Lehmer’s and Deaconescu’s conjectures, as well as various analogue problems concerning Euler’s totient function \varphi(n), Schemmel’s totient function S_{2}(n), Jordan totient function J_k, and the unitary totient function \varphi^{*}(n), we investigate analogous divisibility problems involving the functions \sigma(n), \sigma^{+}(n), and \varphi^{+}(n). Further, we establish some interesting properties of the sequences \left\{\sigma^+(n)\right\}_{n=1}^\infty and \left\{\varphi^+(n)\right\}_{n=1}^\infty, in particular, we prove that each of these sequences contains infinitely many arithmetic progressions of length 3.

Keywords

  • Euler’s totient function
  • Unitary totient function
  • Schemmel’s totient function
  • Jordan totient function
  • Sum of positive divisors function

2020 Mathematics Subject Classification

  • 11A25

References

  1. Burcsi, P., Czirbusz, S., & Farkas, G. (2011). Computational investigation of Lehmer’s totient problem. Annales Universitatis Scientiarum Budapestinensis de Rolando Eötvös Nominatae. Sectio Computatorica, 35, 43–49.
  2. Burek, D., & Żmija, B. (2019). A new upper bound for numbers with the Lehmer property and its application to repunit numbers. International Journal of Number Theory, 15(7), 1463–1468.
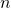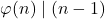  3. Cohen, G. L., & Hagis, P. (1980). On the number of prime factors of n if \varphi(n) \mid (n-1). Nieuw Archief voor Wiskunde, III Series, 28(2), 177–185.
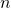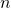  4. Cohen, G. L., & Segal, S. L. (1989). A note concerning those n for which \phi(n)+1 divides n. The Fibonacci Quarterly, 27(3), 285–286.
  5. Deaconescu, M. (2000). Adding units mod 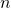n. Elemente der Mathematik, 55(3), 123–127.
  6. Guy, R. K. (1994). Unsolved Problems in Number Theory (2nd ed.). Springer-Verlag.
  7. Hagis, P. (1988). On the equation 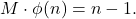M\cdot\phi(n)=n-1. Nieuw Archief voor Wiskunde, IV Series, 6, 255–261.
  8. Hasanalizade, E. (2022). On a conjecture of Deaconescu. Integers, 22, Article ID #A99.
  9. Hernandez, S. H., & Luca, F. (2008). A note on Deaconescu’s result concerning Lehmer’s problem. Integers, 8(1), Article ID #A12.
  10. Lehmer, D. H. (1932). On Euler’s totient function. Bulletin of the American Mathematical Society, 38, 745–751.
  11. Luca, F., & Křížek, M. (2001). On the solutions of the congruence 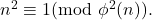n^2\equiv 1 (\mathrm{mod} \ \phi^2(n)). Proceedings of the American Mathematical Society, 129, 2191–2196.
  12. Luca, F., & Pomerance, C. (2011). On composite integers 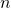n for which 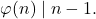\varphi(n)\mid n-1. Boletín de la Sociedad Matemática Mexicana, 17(1), 13–21.
  13. Mandal, S. (2025). A note on Deaconescu’s conjecture. Annals of West University of Timisoara – Mathematics and Computer Science, 61(1), 55–60.
  14. Mandal, S. (2025). A note on newly introduced arithmetic functions φ+ and σ+. Notes on Number Theory and Discrete Mathematics, 31(2), 404–409.
  15. Pomerance, C. (1977). On composite 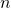n for which \varphi(n)|n-1, II. Pacific Journal of
    Mathematics, 69(2), 177–186.
  16. Sándor, J., & Crstici, B. (2004). Handbook of Number Theory II, Springer.
  17. Sándor, J., & Atanassov, K. (2024). Some new arithmetic functions. Notes on Number Theory and Discrete Mathematics, 30(4), 851–856.
  18. Subbarao, M. V., & Siva Rama Prasad, V. (1985). Some analogues of a Lehmer problem on the totient function. Rocky Mountain Journal of Mathematics, 15(2), 609–620.

Manuscript history

  • Received: 4 August 2025
  • Revised: 5 December 2025
  • Accepted: 8 December 2025
  • Online First: 9 December 2025

Copyright information

Ⓒ 2025 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).

Related papers

Cite this paper

Mandal, S. (2025). Divisibility and sequence properties of σ+ and φ+. Notes on Number Theory and Discrete Mathematics, 31(4), 899-907, DOI: 10.7546/nntdm.2025.31.4.899-907.

Comments are closed.