On special integer linear combinations of terms of rational cycles for the generalized 3x+1 problem

Yagub N. Aliyev
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 3, Pages 658–666
DOI: 10.7546/nntdm.2025.31.3.658-666
Full paper (PDF, 264 Kb)

Details

Authors and affiliations

Yagub N. Aliyev
School of IT and Engineering, ADA University
Ahmadbey Aghaoglu 61, AZ1008 Baku, Azerbaijan

Abstract

In the paper, some special linear combinations of the terms of rational cycles of generalized Collatz sequences are studied. It is proved that for specific choice of the coefficients these linear combinations are integers. The discussed results are demonstrated on some examples. In some particular cases the obtained results can be used to explain some patterns of digits in p-adic representations of the terms of the rational cycles.

Keywords

• 3x+1 problem
• Collatz conjecture
• Rational cycles
• Integer linear combinations

2020 Mathematics Subject Classification

• 11B75
• 11A63
• 11D88

References

1. Aliyev, Y. N. (2020). The 3x + 1 problem for rational numbers: Invariance of periodic sequences in the 3x + 1 problem. Proceedings of IEEE 14th International Conference on Application of Information and Communication Technologies (AICT), 7–20 October 2020, Tashkent, Uzbekistan, pp. 1–4. DOI: 10.1109/AICT50176.2020.9368585.
2. Aliyev, Y. N. (2023). Existence of invariants in periods of generalized Collatz sequences. Proceedings of 5th International Conference on Problems of Cybernetics and Informatics (PCI), 28–30 August 2023, Baku, Azerbaijan, pp. 1–3. DOI: 10.1109/PCI60110.2023.10326001.
3. Böhm, C., & Sontacchi, G. (1978). On the existence of cycles of given length in integer sequences like 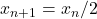if 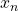even, and 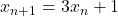. Atti della Accademia Nazionale dei Lincei. Classe di Scienze Fisiche, Matematiche e Naturali. Rendiconti, Serie 8, 64(3), 260–264.
4. Conway, J. H. (2013). On unsettleable arithmetical problems. The American Mathematical Monthly, 120(3), 192–198.
5. Everett, C. J. (1977). Iteration of the number-theoretic function 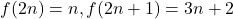. Advances in Mathematics, 25(1), 42–45.
6. Gelfond, A. O. (1954). On the partition of the natural series into classes by the group of linear substitutions. Izvestiya Akademii Nauk SSSR, Seriya Matematicheskaya, 18(4), 297–306.
7. Kaufman, R., & Castañeda, P. (2025). Any positive number is a factor of a number that descends to 1 in the ωx + 1 problem, for odd ω. The College Mathematics Journal, 56(3), 200–202.
8. Kaufman, R., & Lagarias, J. (2023). Problem 12426. In: Problems and Solutions. (Ullman, D. H., Velleman, D. J., Wagon, S., & West, D. B. (eds.)). The American Mathematical Monthly, 130(10), 952–962.
9. Korec, I. (1994). A density estimate for the 3x + 1 problem. Mathematica Slovaca, 44(1), 85–89.
10. Laarhoven, T., & de Weger, B. (2013). The Collatz conjecture and De Bruijn graphs. Indagationes Mathematicae, 24(4), 971–983.
11. Lagarias, J. C. (1990). The set of rational cycles for the 3x + 1 problem. Acta Arithmetica, 56(1), 33–53.
12. Lagarias, J. C. (Ed.). (2010). The Ultimate Challenge: The 3x + 1 Problem. American Mathematical Society, New York.
13. Lehtonen, E. (2008). Two undecidable variants of Collatz’s problems. Theoretical Computer Science, 407(1–3), 596–600.
14. Levy, D. (2004). Injectivity and surjectivity of Collatz functions. Discrete Mathematics, 285(1–3), 191–199.
15. Lutsko, C. (2023). Problem 270. In: Solved and unsolved problems. European
    Mathematical Society Magazine, 127, 53–61.
16. Lutsko, C. (2023). Problem 270 (Solution by the proposer). In: Solved and unsolved problems. European Mathematical Society Magazine, 129, 47–55.
17. Matthews, K., & Watts, A. (1984). A generalization of Hasse’s generalization of the Syracuse algorithm. Acta Arithmetica, 43(2), 167–175.
18. Matthews, K., & Watts, A. (1985). A Markov approach to the generalized Syracuse
    algorithm. Acta Arithmetica, 45(1), 29–42.
19. Pranesachar C. R. (2025). Problem 12426 (Solution). In: Problems and Solutions. (Ullman, D. H., Velleman, D. J., Wagon, S., & West, D. B. (eds.)). The American Mathematical Monthly, 132(7), 706–715.
20. Rouet, J. L., & Feix, M. R. (2002). A generalization of the Collatz problem. Building cycles and a stochastic approach. Journal of Statistical Physics, 107, 1283–1298.
21. Tao, T. (2022). Almost all orbits of the Collatz map attain almost bounded value. Forum of Mathematics, Pi, 10, Article e12.
22. Terras, R. (1976). A stopping time problem on the positive integers. Acta Arithmetica, 30(3), 241–252.

Manuscript history

• Received: 2 December 2024
• Revised: 26 September 2025
• Accepted: 26 September 2025
• Online First: 29 September 2025

Copyright information

Ⓒ 2025 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).