Stoyan Dimitrov
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 3, Pages 481–493
DOI: 10.7546/nntdm.2025.31.3.481-493
Full paper (PDF, 262 Kb)
Details
Authors and affiliations
Stoyan Dimitrov ![]()
![]()
![]()
1 Faculty of Applied Mathematics and Informatics, Technical University of Sofia
8 St. Kliment Ohridski Blvd., Sofia 1756, Bulgaria
2 Department of Bioinformatics and Mathematical Modelling, Institute of Biophysics and Biomedical Engineering, Bulgarian Academy of Sciences
Acad. G. Bonchev Str. Bl. 105, Sofia 1113, Bulgaria
Abstract
In this paper, we revisit Lemma 18 from [2], which concerns a Bombieri–Vinogradov type theorem for exponential sums over primes. We provide a corrected version of the lemma, clarify the original arguments, and address certain inaccuracies present in the initial proof.
Keywords
- Bombieri–Vinogradov theorem
- Exponential sum
- Large sieve
2020 Mathematics Subject Classification
- 11L07
- 11L20
- 11L40
- 11N05
- 11N36
References
- Baier, S., & Zhao, L. (2006). Bombieri–Vinogradov type theorems for sparse sets of moduli. Acta Arithmetica, 125(2), 187–201.
- Dimitrov, S. I. (2022). A ternary Diophantine inequality by primes with one of the form
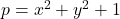 . Ramanujan Journal, 59(2), 571–607.
. Ramanujan Journal, 59(2), 571–607. - Dimitrov, S. I. (2025). The Bombieri–Vinogradov theorem for primes of the form
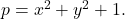 Mediterranean Journal of Mathematics, 22(1), Article ID 9.
Mediterranean Journal of Mathematics, 22(1), Article ID 9. - Dimitrov, S. I. (2025). Barban–Davenport–Halberstam type theorems for exponential sums and Piatetski-Shapiro primes. Results in Mathematics, 80(3), Article ID 87.
- Fouvry, E., & Iwaniec, H. (1980). On a theorem of Bombieri–Vinogradov type. Mathematika, 27(2), 135–152.
- Granville, A., & Shao, X. (2019). Bombieri–Vinogradov for multiplicative functions, and beyond the
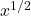 -barrier. Advances in Mathematics, 350, 304–358.
-barrier. Advances in Mathematics, 350, 304–358. - Huxley, M. N., & Iwaniec, H. (1975). Bombieri’s theorem in short intervals. Mathematika, 22(2), 188–194.
- Iwaniec, H., & Kowalski, E. (2004). Analytic Number Theory. Colloquium Publications, Vol. 53, American Mathematical Society, Providence, Rhode Island.
- Karatsuba, A. (1983). Principles of the Analytic Number Theory. Nauka, Moscow (in Russian).
- Li, J., Zhang, M., & Xue, F. (2022). An additive problem over Piatetski-Shapiro primes and almost-primes. Ramanujan Journal, 57(4), 1307–1333.
- Lu, Y. M. (2018). An additive problem on Piatetski-Shapiro primes. Acta Mathematica Sinica, English Series, 34, 255–264.
- Maynard, J. (2019). Primes with restricted digits. Inventiones Mathematicae, 217, 127–218.
- Nath, K. (2024). Primes with a missing digit: Distribution in arithmetic progressions and an application in sieve theory. Journal of the London Mathematical Society, 109(1), Article ID e12837.
- Peneva, T. (2003). An additive problem with Piatetski-Shapiro primes and almost-primes. Monatshefte für Mathematik, 140, 119–133.
- Perelli, A., Pintz, J., & Salerno, S. (1985). Bombieri’s theorem in short intervals. II. Inventiones Mathematicae, 79, 1–9.
- Piatetski-Shapiro, I. I. (1953). On the distribution of prime numbers in sequences of the form
![Rendered by QuickLaTeX.com [f(n)]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-608a57b3f5f53d9e0300c03c6755055c_l3.png) . Matematicheskii Sbornik, 33, 559–566.
. Matematicheskii Sbornik, 33, 559–566. - Tao, Z. (1989). Bombieri’s theorem in short intervals. Acta Mathematica Sinica, 5, 37–47.
- Tenenbaum, G. (1995). Introduction to Analytic and Probabilistic Number Theory. Cambridge University Press, Cambridge.
- Tolev, D. I. (1992). On a Diophantine inequality involving prime numbers. Acta Arithmetica, 613, 289–306.
- Tolev, D. I. (2017). On a Diophantine inequality with prime numbers of a special type. Proceedings of the Steklov Institute of Mathematics, 299, 246–267.
- Vaughan, R. C. (1980). An elementary method in prime number theory. Acta Arithmetica, 37(1), 111–115.
- Wang, X., & Cai, Y. (2011). An additive problem involving Piatetski-Shapiro primes. International Journal of Number Theory, 7(5), 1359–1378.
Manuscript history
- Received: 26 May 2024
- Revised: 24 July 2025
- Accepted: 28 July 2025
- Online First: 4 August 2025
Copyright information
![]() Ⓒ 2025 by the Author.
Ⓒ 2025 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Dimitrov, S. (2025). The Bombieri–Vinogradov theorem for exponential sums over primes. Notes on Number Theory and Discrete Mathematics, 31(3), 481-493, DOI: 10.7546/nntdm.2025.31.3.481-493.


