Identical equations for multiplicative functions

Pentti Haukkanen
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 2, Pages 289–298
DOI: 10.7546/nntdm.2025.31.2.289-298
Full paper (PDF, 210 Kb)

Details

Authors and affiliations

Pentti Haukkanen
Faculty of Information Technology and Communication Sciences,
FI-33014 Tampere University, Finland

Abstract

We examine identical equations for multiplicative functions and certain special cases, such as totients and quadratics. We confine ourselves to identical equations expressing the value (or the value ) nontrivially in terms of the values and where and and holding for all and Particular attention is paid to Busche–Ramanujan type identities. We characterize all functions that satisfy the identical equations. Quasi-multiplicative functions are central to this discussion.

Keywords

• Identical equation
• Busche–Ramanujan identity
• Quasi-multiplicative function
• Multiplicative function
• Quadratic
• Totient

2020 Mathematics Subject Classification

• 11A25

References

1. Apostol, T. M. (1986). Introduction to Analytic Number Theory (3rd printing). Springer.
2. Baum, J. D. (1982). A number-theoretic sum. Mathematics Magazine, 55(2), 111–113.
3. Bellotti, C., & Yang, A. (2024). On the generalised Dirichlet divisor problem. Bulletin of the London Mathematical Society, 56(5), 1859–1878.
4. Busche, E. (1906). Lösung einer Aufgabe über Teileranzahlen. Mitteilungen der Mathematischen Gesellschaft in Hamburg, 4, 229–237.
5. Carroll, T. B., & Gioia, A. A. (1975). On a subgroup of the group of multiplicative arithmetic functions. Journal of the Australian Mathematical Society. Series A, 20(3), 348–358.
6. Gioia, A. A. (1962). On an identity for multiplicative functions. The American Mathematical Monthly, 69(10), 988–991.
7. Gioia, A. A. (1965). The K-product of arithmetic functions. Canadian Journal of Mathematics, 17, 970–976.
8. Haukkanen, P. (1988). Classical arithmetical identities involving a generalization of Ramanujan’s sum. Annales Academiæ Scientiarum Fennicæ. Series A. I. Mathematica Dissertationes, 68, 1–69.
9. Haukkanen, P. (1996). Some characterizations of totients. International Journal of Mathematics and Mathematical Sciences, 19(2), 209–217.
10. Haukkanen, P. (2003). Some characterizations of specially multiplicative functions. International Journal of Mathematics and Mathematical Sciences, 2003(37), 2335–2344.
11. Haukkanen, P. (2012). Extensions of the class of multiplicative functions. East-West Journal of Mathematics, 14(2), 101–113.
12. Haukkanen, P. (2023). Quotients of arithmetical functions under the Dirichlet convolution. Notes on Number Theory and Discrete Mathematics, 29(2), 185–194.
13. Haukkanen, P. (2025). On some classes of multiplicative functions. Aequationes Mathematicae, 99, 531–537.
14. Krishna, K. (1979). A proof of an identity for multiplicative functions. Canadian Mathematical Bulletin, 22(3), 299–304.
15. Lahiri, D. B. (1973). Hypo-multiplicative number-theoretic functions. Aequationes Mathematicae, 9, 184–192.
16. Laohakosol, V., & Pabhapote, N. (2005). Properties of rational arithmetic functions. International Journal of Mathematics and Mathematical Sciences, 2005(24), 3997–4017.
17. Laohakosol, V., & Tangsupphathawat, P. (2018). An identical equation for arithmetic functions of several variables and applications. Notes on Number Theory and Discrete Mathematics, 24(4), 11–17.
18. McCarthy, P. J. (1986). Introduction to Arithmetical Functions. Springer-Verlag, New York.
19. Nicolas, J.-L., & Sitaramaiah, V. (2002). On a class of ψ-convolutions characterized by the identical equation. Journal de Théorie des Nombres de Bordeaux, 14(2), 561–583.
20. Ramanujan, S. (1916). Some formulae in the analytic theory of numbers. The Messenger of Mathematics, 45, 81–84.
21. Sándor, J. (1996). On the arithmetical functions 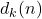and 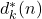. Portugaliae Mathematica, 53(1), 107–115.
22. Selberg, A. (1977). Remarks on multiplicative functions. Number Theory Day (Proc. Conf., Rockefeller Univ., New York, 1976), pp. 232–241, Springer, Berlin, Heidelberg.
23. Shapiro, H. N. (1983). Introduction to the Theory of Numbers. Wiley.
24. Sitaramaiah, V., & Subbarao, M. V. (1996). The identical equation in ψ-products. Proceedings of the American Mathematical Society, 124(2), 361–369.
25. Subbarao, M. V., & Gioia, A. A. (1967). Identities for multiplicative functions. Canadian Mathematical Bulletin, 10(1), 65–73.
26. Tóth, L. (2013). Two generalizations of the Busche–Ramanujan identities.  International Journal of Number Theory, 9(5), 1301–1311.
27. Vaidyanathaswamy, R. (1930). The identical equations of the multiplicative functions. Bulletin of the American Mathematical Society, 36, 762–772.
28. Vaidyanathaswamy, R. (1931). The theory of multiplicative arithmetic functions. Transactions of the American Mathematical Society, 33, 579–662.

Manuscript history

• Received: 10 April 2025
• Accepted: 4 May 2025
• Online First: 9 May 2025

Copyright information

Ⓒ 2025 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).