An identical equation for arithmetic functions of several variables and applications

Vichian Laohakosol and Pinthira Tangsupphathawat
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 24, 2018, Number 4, Pages 11–17
DOI: 10.7546/nntdm.2018.24.4.11-17
Full paper (PDF, 180 Kb)

Details

Authors and affiliations

Vichian Laohakosol
Department of Mathematics, Faculty of Science
Kasetsart University, Bangkok 10900, Thailand

Pinthira Tangsupphathawat
Department of Mathematics, Faculty of Science and Technology
Phranakorn Rajabhat University, Bangkok 10220, Thailand

Abstract

An identical equation for arithmetic functions is proved generalizing the 2-variable case due to Venkataraman. It is then applied to characterize multiplicative functions which are variable-separated, and to deduce interesting properties of generalized Ramanujan sums.

Keywords

• Arithmetic function of several variables
• Identical equation
• Multiplicative functions
• Completely multiplicative functions

2010 Mathematics Subject Classification

• 11A25

References

1. Alkan, E., Zaharescu, A., & Zaki, M. (2005) Arithmetical functions in several variables, Int. J. Number Theory, 1(3), 383–399.
2. Brown, T. C., Hsu, L. C., Wang, J., & Shiue, P. J.-S. (2000) On a certain kind of generalized number-theoretical Möbius function, Math. Sci., 25(2), 72–77.
3. Haukkanen, P. (2018) Derivation of arithmetical functions under the Dirichlet convolution, Int. J. Number Theory, 14(05), 1257–1264.
4. Laohakosol, V., Ruengsinsub, P., & Pabhapote, N. (2006) Ramanujan sums via generalized Möbius functions and applications, Int. J. Math. Math. Sci., Volume 2006, Article ID 60528, 34 pages.
5. Sivaramakrishnan, R. (1989) Classical Theory of Arithmetic Functions, Monographs and Textbooks in Pure and Applied Mathematics, Vol. 126, Marcel Dekker, New York.
6. Souriau, J.-M. (1944) Généralisation de certaines formules arithmétiques d’inversion. Applications, Revue Scientific (Rev. Rose Illus.), 82, 204–211.
7. Tóth, L. (2014) Multiplicative arithmetic functions of several variables: a survey. Mathematics Without Boundaries: Surveys in Pure Mathematics, edited by Themistocles M. Rassias, Panos M. Pardalos, pp. 483-514, Springer, New York.
8. Venkataraman, C. S. (1946) A new identical equation for multiplicative functions of two arguments and its applications to Ramanujan’s sum 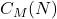, Proc. Ind. Acad. Sci., XXIV(Ser. A), 518–529.