Some fundamental Fibonacci number congruences

Anthony G. Shannon, Tian-Xiao He, Peter J.-S. Shiue and Shen C. Huang
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 1, Pages 27–40
DOI: 10.7546/nntdm.2025.31.1.27-40
Full paper (PDF, 963 Kb)

Details

Authors and affiliations

Anthony G. Shannon
Warrane College, University of New South Wales
Kensington, NSW 2033, Australia

Tian-Xiao He
Department of Mathematics, Illinois Wesleyan University
Bloomington, IL, 61701, United States

Peter J.-S. Shiue
Department of Mathematical Sciences, University of Nevada, Las Vegas
Las Vegas, Nevada, 89154-4020, United States

Shen C. Huang
Department of Mathematical Sciences, University of Nevada, Las Vegas
Las Vegas, Nevada, 89154-4020, United States

Abstract

This paper investigates a number of congruence properties related to the coefficients of a generalized Fibonacci polynomial. This polynomial was defined to produce properties comparable with those of the standard polynomials of some special functions. Some of these properties are compared with known identities, while others are seemingly characteristic of arbitrary order recurrences. These include generalizations of, and analogies for, results of Appell, Bernoulli, Euler, Hilton, Horadam and Williams. In turn, the theorems lead to conjectures for further development.

Keywords

• Congruences
• Recurrence relations
• Fibonacci sequences
• Lucas sequences
• Special functions
• Appell polynomials
• Generalized Fibonacci polynomials

2020 Mathematics Subject Classification

• 11B39
• 11B50
• 11B68

References

1. Aceto, L., Malonek, H. R., & Tomaz, G. (2015). A unified matrix approach to the representation of Appell polynomials. Integral Transforms and Special Functions, 26(6), 426–441.
2. Amdeberhan, T. (2010). A note on Fibonacci-type polynomials. Integers, 10, 13–18.
3. Andrews, G. E., Askey, R., & Roy, R. (1999). Special Functions. Cambridge: Cambridge University Press.
4. Asveld, P. R. J. (1989). Fibonacci-like differential equations with a polynomial nonhomogeneous part. The Fibonacci Quarterly, 27(4), 303–309.
5. Bundschuh, P., & Shiue, P. J.-S. (1973). Solution of a problem on the uniform distribution of integers. Atti della Accademia Nazionale dei Lincei. Classe di Scienze Fisiche, Matematiche e Naturali. Rendiconti, Serie 8, 55(3–4), 172–177.
6. Carlitz, L. (1960). Some arithmetic sums connected with the greatest integer function. Mathematica Scandinavica, 8, 59–64.
7. Carlitz, L. (1965). Recurrences for the Bernoulli and Euler numbers. II. Mathematische Nachrichen, 29(3–4), 151–160.
8. Cigler, J. (2003). A new class of q-Fibonacci polynomials. The Electronic Journal of Combinatorics, 10, Article #R19.
9. Hilton, A., Dresel, L. A. G., & Daykin, D. (1974). The structure of second order sequences in a finite field. Journal für die reine und angewandte Mathematik, 270, 77–96.
10. Hoggatt, V. E., Jr., & Bicknell, M. (1973). Roots of Fibonacci polynomials. The Fibonacci Quarterly, 11(3), 271–274.
11. Hopkins, B., & Tangboonduangjit, A. (2018). Fibonacci-producing rational polynomials. The Fibonacci Quarterly, 56(4), 303–312.
12. Horadam, A. F. (1965). Generating functions for powers of a certain generalized sequence of numbers. Duke Mathematical Journal, 32(3), 437–446.
13. Horadam, A. F. (1965). Basic properties of a certain generalized sequence of numbers. The Fibonacci Quarterly, 3(3), 161–176.
14. Hunter, J. (1964). Number Theory. Edinburgh: Oliver and Boyd, 22–23.
15. Kuipers, L., Shiue, P. J.-S. (1972). A distribution property of the sequence of Fibonacci numbers. The Fibonacci Quarterly, 10(4), 375–376, 392.
16. Lay, D. C., Lay, S. R., & McDonald, J. J. (2021). Linear Algebra and Its Applications. London: Pearson.
17. Lehman, J. L., & Triola, C. (2010). Recursive sequences and polynomial congruences. Involve, 3(2), 129–148.
18. Lucas, É. (1891). Théorie des Nombres. Paris: Gauthier Villars.
19. Melham, R. S., & Shannon, A. G. (1995). Generalizations of some simple congruences. The Fibonacci Quarterly, 33(2), 126–130.
20. Nalli, A., & Haukkanen, P. (2009). On generalized Fibonacci and Lucas polynomials. Chaos, Solitons & Fractals, 42(5), 3179–3186.
21. Niederreiter, H. (1972). Distribution of Fibonacci numbers mod 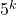. The Fibonacci Quarterly, 10(4), 373–374.
22. Shannon, A. G. (1975). Fibonacci analogs of the classical polynomials. Mathematics Magazine, 48(3), 123–130.
23. Shannon, A. G. (2013). The sequences of Horadam, Williams and Philippou as generalized Lucas sequences. Advanced Studies in Contemporary Mathematics, 23(3), 551–558.
24. Shannon, A. G., Cook, C. K., & Hillman, R. A. (2013). Some aspects of Fibonacci polynomial congruences. Annales Mathematicae et Informaticae, 41, 211–217.
25. Shannon, A. G., Deveci, Ö., & Erdağ, Ö. (2019). Generalized Fibonacci numbers and Bernoulli polynomials. Notes on Number Theory and Discrete Mathematics, 25(1), 193–198.
26. Shannon, A. G., Horadam, A. F. (1971). Generating functions for powers of third order recurrence sequences. Duke Mathematical Journal, 38(4), 791–794.
27. Shannon, A. G., Horadam, A. F., & Collings, S. N. (1974). Some congruences for Fibonacci numbers. The Fibonacci Quarterly, 12(4), 351–354, 362.
28. Sun, B. Y., Xie, M. H. Y., & Yang, A. L. B. (2016). Melham’s conjecture on odd power sums of Fibonacci numbers. Quaestiones Mathematicae, 39(7), 945–957.
29. Ward, M. (1931). The distribution of residues in a sequence satisfying a linear recurrence relation. Transactions of the American Mathematical Society, 33(1), 166–190.
30. Ward, M. (1936). The null divisors of linear recurring series. Duke Mathematical Journal, 2(3), 472–476.
31. Williams, H. C. (1972). On a generalization of the Lucas functions. Acta Arithmetica, 20(1), 33–51.

Manuscript history

• Received: 28 October 2024
• Revised: 26 March 2025
• Accepted: 28 March 2025
• Online First: 28 March 2025

Copyright information

Ⓒ 2025 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).