Taekyun Kim and Dae San Kim
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 1, Pages 166–180
DOI: 10.7546/nntdm.2025.31.1.166-180
Full paper (PDF, 263 Kb)
Details
Authors and affiliations
Taekyun Kim ![]()
![]()
Department of Mathematics, Kwangwoon University
Seoul 139-701, Republic of Korea
Dae San Kim ![]()
![]()
Department of Mathematics, Sogang University
Seoul 121-742, Republic of Korea
Abstract
In this paper, we derive by using elementary methods some continued fractions, certain identities involving derivatives of ![]() , several expressions for
, several expressions for ![]() and an identity for
and an identity for ![]() , from a series expansion of
, from a series expansion of ![]() , which gives the product expansion of the cosine function.
, which gives the product expansion of the cosine function.
Keywords
- Continued fraction
- Product expansion
- Bernoulli numbers
- Euler numbers
2020 Mathematics Subject Classification
- 11A55
- 11B68
References
- Apéry, R. (1979). Irrationalité
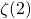 et
et 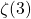 . Astérisque, 61, 11–13.
. Astérisque, 61, 11–13. - Chaturvedi, A., & Rai, P. (2020). Relations between generalized Hermite based Apostol–Bernoulli, Euler and Genocchi polynomials. Proceedings of the Jangjeon Mathematical Society, 23(1), 53–63.
- Ciaurri, Ó. (2015). Euler’s product expansion for the sine: An elementary proof. The American Mathematical Monthly, 122(7), 693–695.
- Dolgy, D. V., Kim, W., & Lee, H. (2023). A note on generalized degenerate Frobenius–Euler–Genocchi polynomials. Advanced Studies in Contemporary Mathematics, 33(2), 111–121.
- Dutka, J. (1982). Wallis’s product, Brouncker’s continued fraction, and Leibniz’s series. Archive for History of Exact Sciences, 26(2), 115–126.
- Gaboury, S., Tremblay, R., & Fugère, B.-J. (2014). Some explicit formulas for certain new classes of Bernoulli, Euler and Genocchi polynomials. Proceedings of the Jangjeon Mathematical Society, 17(1), 115–123.
- Kim, D. S., & Kim, T. K. (2023). Normal ordering associated with λ-Whitney numbers of the first kind in λ-shift algebra. Russian Journal of Mathematical Physics, 30(3), 310–319.
- Kim, T. (2008). Euler numbers and polynomials associated with zeta functions. Abstract and Applied Analysis, 2008, Article ID 581582.
- Kim, T. (2015). Degenerate Euler zeta function. Russian Journal of Mathematical Physics, 22(4), 469–472.
- Kim, T., & Kim, D. S. (2024). Generalization of Spivey’s recurrence relation. Russian Journal of Mathematical Physics, 31(2), 218–226.
- Kim, T., & Kim, D. S. (2024). Probabilistic Bernoulli and Euler polynomials. Russian Journal of Mathematical Physics, 31(1), 94–105.
- Kim, T., Kim, D. S., Kwon, J., & Lee, H. (2023). Lerch-harmonic numbers related to Lerch transcendent. Mathematical and Computer Modelling of Dynamical Systems, 29(1), 315–323.
- Kortram, R. A. (1996). Simple proofs for
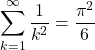 and
and 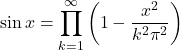 . Mathematics Magazine, 69(2), 122–125.
. Mathematics Magazine, 69(2), 122–125. - Lange, L. J. (1999). An elegant continued fraction for π. The American Mathematical Monthly, 106(5), 456–458.
- Roman, S. (1984). The Umbral Calculus. (Pure and Applied Mathematics, Vol. 111). Academic Press, London.
- Şen, E. (2013). Theorems on Apostol–Euler polynomials of higher order arising from Euler basis. Advanced Studies in Contemporary Mathematics, 23(2), 337–345.
- Shiratani, K. (1973). On Euler numbers. Memoirs of the Faculty of Science, Kyushu University, Series A, 27(1), 1–5.
- Simsek, Y. (2013). Interpolation functions of the Eulerian type polynomials and numbers. Advanced Studies in Contemporary Mathematics, 23(2), 301–307.
- Whittaker, E. T., & Watson, G. N. (2021). A Course of Modern Analysis: An Introduction to the General Theory of Infinite Processes and of Analytic Functions with an Account of the Principal Transcendental Functions (5th ed., Moll, V. H. Moll, Ed.). Cambridge University Press, Cambridge.
- Yun, S. J., Park, J.-W., & Kwon, J. (2020). Symmetric identities of type 2 Bernoulli and Euler polynomials under
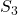 . Advanced Studies in Contemporary Mathematics, 30(3), 407–415.
. Advanced Studies in Contemporary Mathematics, 30(3), 407–415. - Zill, D., Wright, W. S., & Cullen, M. R. (2011). Advanced Engineering Mathematics. Jones & Bartlett Learning, Burlington.
Manuscript history
- Received: 23 January 2025
- Revised: 27 April 2025
- Accepted: 28 April 2025
- Online First: 28 April 2025
Copyright information
![]() Ⓒ 2025 by the Authors.
Ⓒ 2025 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Kim, T., & Kim, D. S. (2025). Some formulas related to Euler’s product expansion for cosine function. Notes on Number Theory and Discrete Mathematics, 31(1), 166-180, DOI: 10.7546/nntdm.2025.31.1.166-180.


