A. Bërdëllima
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 1, Pages 15–26
DOI: 10.7546/nntdm.2025.31.1.15-26
Full paper (PDF, 262 Kb)
Details
Authors and affiliations
A. Bërdëllima ![]()
![]()
Faculty of Engineering, German International University in Berlin
Am Borsigturm 162, 13507, Berlin, Germany
Abstract
We revisit a classical theorem of Chebyshev about distribution of primes on intervals ![]()
![]() , and prove a generalization of it. Extending Erdős’ arithmetical-combinatorial argument, we show that for all
, and prove a generalization of it. Extending Erdős’ arithmetical-combinatorial argument, we show that for all ![]() , there is
, there is ![]() such that the intervals
such that the intervals ![]() contain a prime for all
contain a prime for all ![]() . A quantitative lower bound is derived for the number of primes on such intervals. We also give numerical upper bounds for
. A quantitative lower bound is derived for the number of primes on such intervals. We also give numerical upper bounds for ![]() for
for ![]() , and we draw comparisons with existing results in the literature.
, and we draw comparisons with existing results in the literature.
Keywords
- Bertrand’s postulate
- Chebyshev’s theorem
- Distribution of primes
2020 Mathematics Subject Classification
- 11A41
- 11-03
References
- Apostol, T. M. (1976). Introduction to Analytic Number Theory. New York: Springer-Verlag.
- El Bachraoui, M. (2006). Primes in the interval
![Rendered by QuickLaTeX.com [2n,3n]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-4bc140bb57765f7eae970ae2dbdcde7e_l3.png) . International Journal of Contemporary Mathematical Sciences, 1(13–16), 617–621.
. International Journal of Contemporary Mathematical Sciences, 1(13–16), 617–621. - Bertrand, J. (1845). Mémoire sur le nombre de valeurs que peut prendre une fonction quand on y permute les lettres qu’elle renferme. Journal de l’Ecole Royale Polytechnique, 30(18), 123–140 (in French).
- Broadbent, S., & Kadiri, H.,& Lumley, A.,& Ng, N.,& Wilk, K. (2021). Sharper bounds for the Chebyshev function
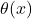 . Mathematics of Computation, 90(331), 2281–2315.
. Mathematics of Computation, 90(331), 2281–2315. - Cully-Hugill, M., & Lee, E. S. (2022). Explicit interval estimates for prime numbers. Mathematics of Computation, 91(336), 1955–1970.
- Cully-Hugill, M., & Lee, E. S. (2024). Corrigendum to ‘Explicit interval estimates for prime numbers’. Mathematics of Computation, 93(346), 1019–1025.
- Dusart, P. (2018). Explicit estimates of some functions over primes. Ramanujan Journal, 45, 227–251.
- Dusart, P. (2010). Estimates of some functions over primes without R.H. Preprint. https://arxiv.org/abs/1002.0442.
- Erdős, P. (1932). Beweis eines Satzes von Tschebyschef. Acta Scientiarum
Mathematicarum, 5(3–4), 194–198 (in German). - Hanson, D. (1973). On a theorem of Sylvester and Schur. Canadian Mathematical Bulletin, 16(2), 195–199
- Nagura, J. (1952). On the interval containing at least one prime number. Proceedings of the Japan Academy, Ser. A, Mathematical Sciences, 28(4), 177–181.
- Ramanujan, S. (1919). A proof of Bertrand’s postulate. Journal of the Indian Mathematical Society, 11, 181–182.
- Ramaré, O., & Saouter, Y. (2003). Short effective intervals containing primes. Journal of Number Theory, 98, 10–33.
- Rosser, J. B., & Schoenfeld, L. (1962). Approximate formulas for some functions of prime numbers. Illinois Journal of Mathematics, 6(1), 64–94.
- Rosser, J. B., & Schoenfeld, L. (1975). Sharper Bounds for the Chebyshev Functions
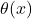 and
and 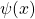 . Mathematics of Computation, 29(129), 243–269.
. Mathematics of Computation, 29(129), 243–269. - Schoenfeld, L. (1976). Sharper bounds for the Chebyshev functions
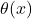 and
and 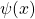 , II. Mathematics of Computation, 30(134), 337–360.
, II. Mathematics of Computation, 30(134), 337–360. - Shevelev, V., Greathouse, C. R., IV, & Moses, P. J. C. (2013). On intervals
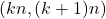 containing a prime for all
containing a prime for all 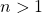 . Journal of Integer Sequences, 16, Article 13.7.3.
. Journal of Integer Sequences, 16, Article 13.7.3. - Sylvester, J. J. (1892). On arithmetical series. Messenger of Mathematics, 21, 1–19.
- Tchebichef, P. (1852). Mémoire sur les nombres premiers. Journal de Mathématiques Pures et Appliquées, Série 1, 17, 366–390 (in French).
Manuscript history
- Received: 16 May 2024
- Revised: 18 October 2024
- Accepted: 26 March 2025
- Online First: 28 March 2025
Copyright information
![]() Ⓒ 2025 by the Author.
Ⓒ 2025 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Bërdëllima, A. (2025). A note on Chebyshev’s theorem. Notes on Number Theory and Discrete Mathematics, 31(1), 15-26, DOI: 10.7546/nntdm.2025.31.1.15-26.


