Krassimir T. Atanassov
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 1, Pages 146–156
DOI: 10.7546/nntdm.2025.31.1.146-156
Full paper (PDF, 243 Kb)
Details
Authors and affiliations
Krassimir T. Atanassov 
Bioinformatics and Mathematical Modelling Department, Institute of Biophysics and Biomedical Engineering, Bulgarian Academy of Sciences
105 Acad. G. Bonchev Str., 1113 Sofia, Bulgaria
Abstract
In the previous author’s research, the set of 
‘s for natural numbers 
was constructed. For this set it was proved that it is a commutative semi-group. The condition for which it is a monoid was given. The present leg of research continues by demonstrating that for any 
is a lattice, and by the introduction of four new operations over the elements of .
Keywords
- Natural numer
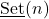
2020 Mathematics Subject Classification
- 11A25
References
- Atanassov, K. (2020). Objects generated by an arbitrary natural number. Notes on Number Theory and Discrete Mathematics, 26(4), 57–62.
- Atanassov, K. (2022). Objects generated by an arbitrary natural number. Part 2: Modal aspect. Notes on Number Theory and Discrete Mathematics, 28(3), 558–563.
- Atanassov, K. (2023). Objects generated by an arbitrary natural number. Part 3: Standard modal-topological aspect. Notes on Number Theory and Discrete Mathematics, 29(1), 171–180.
- Atanassov, K. (2023). Objects generated by an arbitrary natural number. Part 4: New aspects. Notes on Number Theory and Discrete Mathematics, 29(3), 589–597.
- Atanassov, K. (2024). On the set of Set(n)’s. Notes on Number Theory and Discrete Mathematics, 30(3), 590–594.
- Atanassov, K., & Sándor, J. (2023). On a modification of Set(n). Notes on Number Theory and Discrete Mathematics, 29(4), 813–819.
- Birkhoff, G. (1967). Lattice Theory (3rd ed.). Providence, Rhode Island.
- MacLane, S., & Birkhoff, G. (1999). Algebra (3rd ed.). Providence, AMS Chelsea Publ.
- Sándor, J., & Crstici, B. (2005). Handbook of Number Theory. II. Springer Verlag, Berlin
Manuscript history
- Received: 21 December 2024
- Revised: 4 April 2025
- Accepted: 25 April 2025
- Online First: 25 April 2025
Copyright information
Ⓒ 2025 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
- Atanassov, K. (2020). Objects generated by an arbitrary natural number. Notes on Number Theory and Discrete Mathematics, 26(4), 57–62.
- Atanassov, K. (2022). Objects generated by an arbitrary natural number. Part 2: Modal aspect. Notes on Number Theory and Discrete Mathematics, 28(3), 558–563.
- Atanassov, K. (2023). Objects generated by an arbitrary natural number. Part 3: Standard modal-topological aspect. Notes on Number Theory and Discrete Mathematics, 29(1), 171–180.
- Atanassov, K. (2023). Objects generated by an arbitrary natural number. Part 4: New aspects. Notes on Number Theory and Discrete Mathematics, 29(3), 589–597.
- Atanassov, K. (2024). On the set of Set(n)’s. Notes on Number Theory and Discrete Mathematics, 30(3), 590–594.
- Atanassov, K., & Sándor, J. (2023). On a modification of Set(n). Notes on Number Theory and Discrete Mathematics, 29(4), 813–819.
Cite this paper
Atanassov, K. T. (2025). On the set of Set(n)’s. Part 2. Notes on Number Theory and Discrete Mathematics, 31(1), 146-156, DOI: 10.7546/nntdm.2025.31.1.146-156.
